Приёмы письменного деления на однозначное число. Проверка деления умножением

Здравствуйте, здравствуйте, друзья.

Сегодня мы продолжим разговор о приёмах письменного деления на однозначное число. На прошлом уроке мы познакомились с простейшим делением трёхзначного числа на однозначное, при котором каждый разряд делимого без остатка делился на делитель.

Но далеко не всегда деление может быть таким простым. Сегодня я предлагаю вам разобрать вот эти примеры:

Давайте попробуем разделить пятьсот шестьдесят восемь на два.

Кстати, поскольку мы делим не всё число сразу, а как бы по частям, то каждую такую часть делимого мы можем назвать «неполное делимое».

Не забыли? Деление мы начинаем не с единиц, а с наибольшего разряда.

В числе пятьсот шестьдесят восемь – это сотни. Их пять. Пять – это первое неполное делимое. Пять на два не делится без остатка. Но мы знаем, что два содержится в числе пять два раза. Записываем двойку в частное, а теперь умножим её на делитель.

Полученное произведение записываем под сотнями делимого и вычитаем из них. Разность чисел пять и четыре, один – это остаток. Вы помните, что остаток должен быть меньше делителя? Сравниваем остаток с делителем. Остаток – один, меньше делителя – два.  Всё верно.

Чтобы разделить десятки, перенесём под черту шестёрку и запишем справа от единицы. Одна сотня остатка и шесть десятков – это шестнадцать десятков. Это второе неполное делимое.

Делим шестнадцать на два, получится восемь. Записываем восемь в частном. Проверяем, умножая восемь на два. Шестнадцать. Записываем под вторым неполным делимым и выполняем вычитание. Здесь вычитание без остатка, то есть получается нуль. Но нуль мы не пишем, потому что ещё предстоит делить единицы. Переносим вниз восемь единиц, третье неполное делимое. Делим на два – четыре. Записали в частное. Теперь умножаем четыре на два. Восемь записываем под третьим неполным делимым. Вычитаем. Получился нуль. Его мы записываем, так как разделили всё число.

Ответ: двести восемьдесят четыре.

А верно ли мы выполнили деление? Проверить это можно умножением.

Умножаем двести восемьдесят четыре на два. Умножение начинаем с единиц. Дважды четыре – восемь. Умножаем десятки. Восемью четыре – шестнадцать. Шесть десятков пишем, одну сотню запоминаем. Умножаем сотни. Дважды два – четыре, и ещё одна сотня – пять. Ответ: пятьсот шестьдесят восемь.

Всё верно. Можно решать следующий пример.

Шестьсот семьдесят два разделить на три.

Первое неполное делимое – шесть. Делим на три, получится два. Умножаем два на три. Это шесть. Вычитаем из шести шесть – нуль. Его мы не пишем. Переносим вниз второе неполное делимое – семь. Оно не делится без остатка на три, но три содержится в семи два раза. Умножаем два на три – шесть. Вычитаем из семи.

Остаток один. Он меньше делителя.

Переносим вниз два, и третье неполное делимое – двенадцать. Делим его на три, получается четыре. Четырежды три – двенадцать. Вычитаем.

Остаток – нуль. Ответ: двести двадцать четыре.

Проверяем деление умножением.

Всё верно. И этот пример решён.

А теперь давайте шестьсот двадцать пять разделим на пять.

Первое неполное делимое шесть не делится без остатка на пять. Пять содержится в шести один раз. Пишем единицу в частном. Умножаем один на пять, получается пять. Вычитаем из шести пять, остаток – один. Он меньше делителя.

Переносим вниз два десятка. Второе неполное делимое – двенадцать. Оно тоже не делится на пять без остатка. Но пять содержится в двенадцати два раза. Пишем два. Умножаем два на пять. Это десять. Вычитаем его из двенадцати. Остаток – два. Он меньше делителя. Переносим вниз единицы – пять. Третье неполное делимое – двадцать пять. Делим его на пять, получилось пять. Умножаем на делитель. Двадцать пять. Вычитаем из неполного делимого. Записываем нуль. Деление окончено. Ответ: сто двадцать пять. Ну и, конечно же, деление проверим умножением. Умножаем сто двадцать пять на пять.

Ай да Матюша! Ай да молодец! Я всё решил без ошибок. Хотя, честно признаюсь,  бывают и у меня ошибки. Как-то однажды решал я пример на деление, и вот что у меня получилось. Кошмар! Частное оказалось больше делимого! А что же я сделал не так?

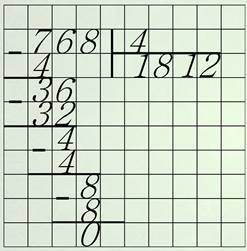
Попробуйте найти мою ошибку. Ну что, поняли, где я её допустил? Посмотрите, разделив второе неполное делимое – тридцать шесть на четыре, я  получил восемь. Восемь умножил на четыре – тридцать два. При вычитании получился остаток четыре. Его я тоже разделил на делитель и получил лишнюю цифру, один, в частном. Если бы я не поленился и сравнил остаток четыре с делителем, то заметил бы, что остаток равен делителю. А это недопустимо! Остаток не должен быть больше или равен делителю. Он обязательно должен быть меньше делителя. Большой остаток подсказывает, что восьми в частном маловато. Если бы я взял не восемь, а девять, то при умножении получилось бы тридцать шесть. И весь пример выглядел бы вот так:

И ещё, не допустить подобных ошибок помогает предварительный подсчёт количества цифр в частном. Так как в делимом три разряда, и каждый из них можно разделить на делитель, хоть и с остатком, то и в частном тоже должно быть три цифры. Но, главное, поймите: при делении целых чисел частное обычно бывает меньше делимого, поэтому в частном не бывает больше цифр, чем в делимом. Конечно, если делится нацело, без остатка.

Иногда, правда делимое и частное равны, если делитель равен единице.

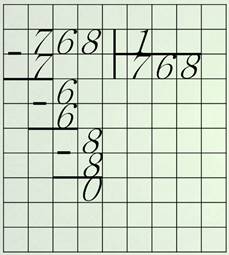
Ну вот мы сегодня и разобрали некоторые случаи деления трёхзначных чисел на однозначные. Постарайтесь запомнить, ребята:

* Если неполное делимое делится с остатком, то следующую цифру из делимого переносим вниз и записываем справа от остатка. Полученное число будет следующим неполным делимым.

Не забывайте каждый раз после вычитания из неполного делимого сравнить полученный остаток с делителем. Остаток обязательно должен быть меньше делителя.

А я прощаюсь с вами, друзья.