Умножение дробей. Возведение дроби в степень

Для начала давайте вспомним правило умножения обыкновенных дробей.          

Для того чтобы умножить дробь на дробь, надо числитель умножить на числитель, а знаменатель на знаменатель и первое произведение записать в числителе новой дроби, второе – в знаменателе.

Например

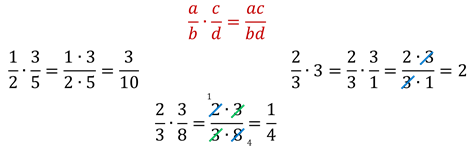
Аналогичным образом происходит умножение рациональных дробей. Давайте докажем, что это правило на самом деле действует при умножении рациональных дробей.

Иначе говоря, докажем, что произведение двух рациональных дробей тождественно равно дроби, у которой числитель равен произведению числителей, а знаменатель – произведению знаменателей перемножаемых дробей при любых допустимых значениях переменных, кроме b равное нулю и d равное нулю.

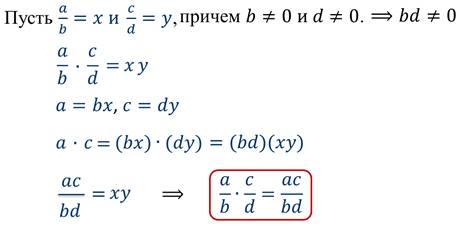
Получили, что равенство верно при любых допустимых значениях переменных, т.е. является тождеством.

Правило умножения рациональных дробей:

Чтобы умножить дробь на дробь, нужно перемножить их числители и перемножить их знаменатели и первое произведение записать числителем, а второе – знаменателем дроби.

В буквенном виде это правило записывают так:  

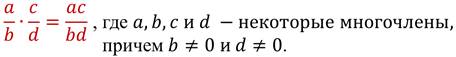
Это правило выполняется и когда произведение трёх и более рациональных дробей.

Прежде чем выполнять умножение рациональных дробей, полезно их числители и знаменатели разложить на множители. Это облегчит сокращение той рациональной дроби, которая получится в результате умножения.

Пример 1: умножить дроби.

Решение:

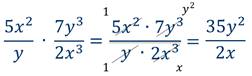
Пример 2: умножить дроби.

Решение:

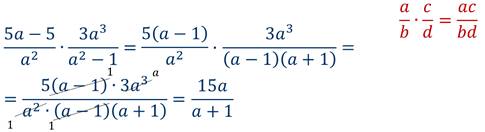
Пример 3: Представить произведение дробей в виде рациональной дроби.

Решение:

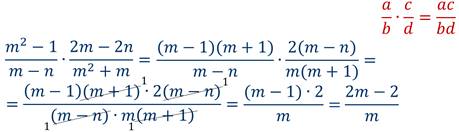
Пример 4: выполнить умножение.

Решение:

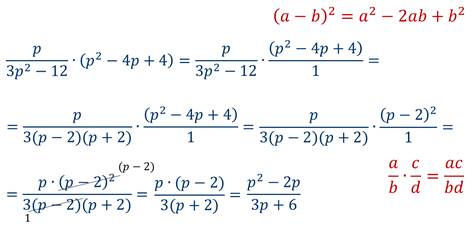
Теперь рассмотрим, как выполняется возведение рациональной дроби в степень.

Проверим это равенство на конкретных примерах.

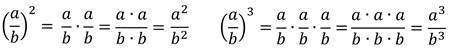
Правило возведения рациональной дроби в степень:

Чтобы возвести дробь в степень, надо возвести в эту степень числитель и знаменатель и первый результат записать в числителе, а второй в знаменателе дроби.

Пример 5: возвести в третью степень дробь.

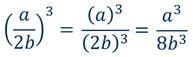
Пример 6: возвести во вторую степень дробь.  

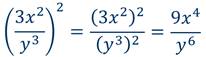
Пример 7:

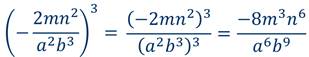
Итоги

Чтобы умножить дробь на дробь, нужно перемножить их числители и перемножить их знаменатели и первое произведение записать числителем, а второе – знаменателем дроби.

Чтобы возвести дробь в степень, надо возвести в эту степень числитель и знаменатель и первый результат записать в числителе, а второй в знаменателе дроби.