Параллельность трех прямых

Вопросы занятия:

·     докажем лемму о двух параллельных прямых, пересекающих плоскость;

·     докажем теорему о двух прямых, параллельных третьей прямой.

Материал урока.

Ранее мы с вами уже узнали, какие прямые называют параллельными в пространстве. Напомню, что две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются. Также мы с вами доказали теорему о том, что через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна.

Теперь докажем лемму о пересечении плоскости параллельными прямыми.

Если одна из двух параллельных прямых пересекает плоскость, то и другая прямая пересекает эту плоскость.

Доказательство. Пусть прямые а и b – параллельные. И одна из них, например, прямая а – пересекает плоскость α в точке М. Докажем, что прямая b также пересекает плоскость α, т.е. имеет с ней только одну общую точку.

Рассмотрим плоскость β, в которой лежат параллельные прямые а и b. Так как две различные плоскости α и β имеют общую точку М, то по третьей аксиоме (если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей) они пересекаются по некоторой прямой p. Эта прямая лежит в плоскости β и пересекает прямую а в точке М. Значит, она пересекает и прямую b, параллельную прямой а, в некоторой точке N. Прямая p лежит также в плоскости α, поэтому точка N – точка плоскости α. Следовательно, N – общая точка прямой b и плоскости α.

Докажем теперь, что прямая b не имеет других общих точек с плоскостью α, кроме точки N. Это и будет означать, что прямая b пересекает плоскость α. Действительно, если бы прямая b имела еще одну общую точку с плоскостью α, то она целиком лежала бы в плоскости α, а следовательно, была бы общей прямой плоскостей α и β, т.е. совпадала бы с прямой p. Но это невозможно, так как по условию прямые а и b параллельны, а прямые а и p пересекаются. Таким образом, прямая b имеет с плоскостью α единственную общую точку N, т.е. пересекается с плоскостью альфа в точке N. Лемма доказана.

Из курса планиметрии вы помните, что если три прямые лежат в одной плоскости и две из них параллельны третьей прямой, то эти две прямые параллельны. Аналогичное утверждение справедливо и для трех прямых в пространстве. Сформулируем и докажем это утверждение.

Теорема (Признак параллельности прямых).

Если две прямые параллельны третьей прямой, то они параллельны.

Доказательство. Пусть прямая а параллельна прямой c, прямая b параллельна прямой cэ. Докажем, что прямая а параллельна прямой b. Для этого нам нужно доказать, что прямые а и b лежат в одной плоскости и не пересекаются.

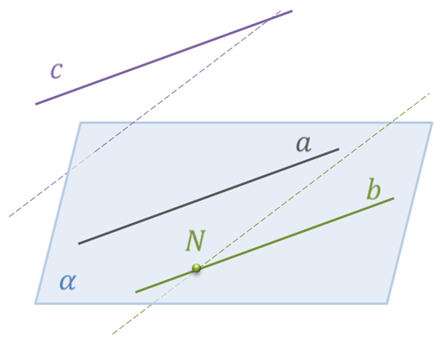
Отметим некоторую точку N на прямой b. Мы знаем, что через прямую и не лежащую на ней точку проходит плоскость, и притом только одна. Значит, через прямую а и точку N, не лежащую на ней, проходит единственная плоскость. Обозначим буквой α плоскость, проходящую через прямую а и точку N. Докажем, что прямая b лежит в плоскости α. Допустим, что прямая b пересекает плоскость α. Тогда по лемме о  пересечении плоскости параллельными прямыми прямая c также пересекает плоскость α. Но так как прямые а и c параллельны по условию, то и прямая а должна пересекать плоскость α, что противоречит тому, что прямая а лежит в плоскости α.

Прямые а и b не пересекаются, так как в противном случае через точку их пересечения проходили бы две прямые а и b, параллельные прямой c, что невозможно. Теорема доказана.  

Задание. Дан параллелепипед . Докажите, что прямые .

Доказательство. Рассмотрим четырехугольник AA₁D₁D.

Он является параллелограммом по определению параллелепипеда. Значит, прямая AD параллельна прямой A₁D₁.

Рассмотрим четырехугольник A₁B₁C₁D₁. Он также является параллелограммом по определению параллелепипеда. Следовательно, прямая A₁D₁ параллельна прямой B₁C₁. Тогда по признаку параллельности прямых (если две прямые параллельны третьей прямой, то они параллельны), имеем прямая AD параллельна прямой B₁C₁. Что и требовалось доказать.

Задание. В основании прямоугольного параллелепипеда  лежит квадрат со стороной  см, а длина бокового ребра параллелепипеда равна  см. Точки , ,  и  являются серединами отрезков , ,  и  соответственно. Вычислите периметр четырехугольника .

Решение.

Подведем итоги урока. На этом уроке мы продолжили рассматривать параллельные прямые в пространстве. А именно, рассмотрели параллельность трех прямых. Доказали лемму о том, что если одна из двух параллельных прямых пересекает плоскость, то и другая прямая пересекает эту плоскость. А затем с ее помощью доказали теорему о двух прямых, параллельных третьей прямой.