Вопросы занятия:
· рассмотрим понятие параллельных прямых в пространстве;
· дадим определение параллельных прямых в пространстве;
· докажем теорему единственности прямой, параллельной данной.
Материал урока.
Ранее в планиметрии мы с вами уже рассматривали взаимное расположение двух прямых на плоскости. Напомню, что возможны три случая:
Первый случай. Прямые параллельны, т.е. две прямые не имеют общих точек.
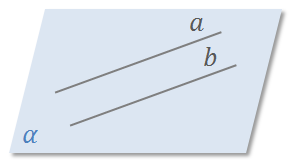
Второй случай. Прямые пересекаются, т.е. две прямые имеют одну общую точку.
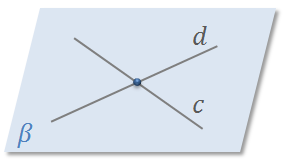
И третий случай. Прямые совпадают, т.е. имеют более чем одну общую точку.
Теперь перейдем к стереометрии. Напомню, что стереометрия изучает свойства фигур в пространстве.
Рассмотрим прямоугольный параллелепипед ABCDA1B1C1D1. Как вы уже знаете, параллелепипед – это пространственное тело.
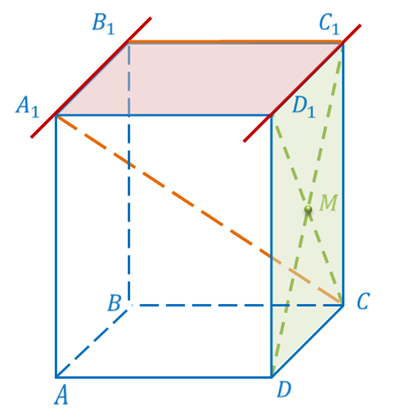
Прямые, на которых лежат его ребра, например, A1B1, D1C1 и DC – параллельны. Прямые, через которые проходят диагонали его грани, например, D1C1 и DC – пересекаются. А вот прямые, на которых лежат диагональ параллелепипеда A1C и ребро B1C1 называются скрещивающимися.
Сделаем вывод: две прямые в пространстве могут пересекаться, быть параллельными или скрещиваться.
Пересекающиеся и параллельные прямые задают некоторую плоскость. Скрещивающиеся прямые – это прямые, через которые нельзя провести плоскость.
Давайте подробно остановимся на случае с параллельными прямыми в пространстве.
Определение. Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
Обратите внимание, что оговорка «если они лежат в одной плоскости» в определении очень важна. Так как в стереометрии мы с вами рассматриваем трехмерное пространство и, если две прямые лежат в разных плоскостях, то нельзя говорить про их параллельность. Параллельными прямые могут быть только если лежат в одной плоскости.
Если прямые а и b параллельны,
то это обозначают следующим образом 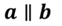 . Читают «прямая а параллельна прямой b».
. Читают «прямая а параллельна прямой b».
Посмотрим внимательно на рисунок.
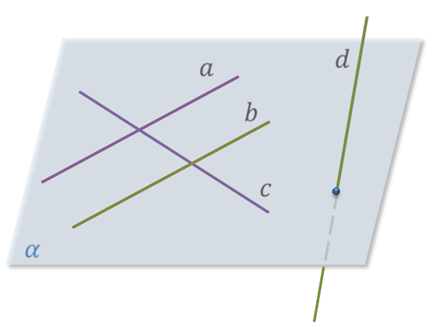
Здесь прямые а и b параллельны. А вот прямые а и c, b и d– не параллельны.
Приведем несколько примеров параллельных прямых в пространстве. Знакомые каждому железнодорожные рельсы.

На ровной местности их можно рассматривать, как параллельные прямые.
А посмотрите внимательно на свою тетрадь. Обратите внимание, противоположные края тетрадного листа также лежат на параллельных прямых.

Прямые, по которым плоскость стены комнаты пересекает плоскости потолка и пола. Они также являются параллельными.

Запишем определения. Два отрезка (луча) называются параллельными, если они лежат на параллельных прямых.

Отрезок (луч) называется параллельным данной прямой, если он лежит на прямой, параллельной данной.
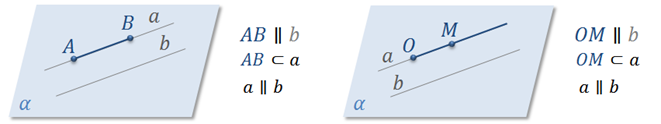
Справедлива теорема о параллельности прямых. Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна.
Докажем эту теорему.
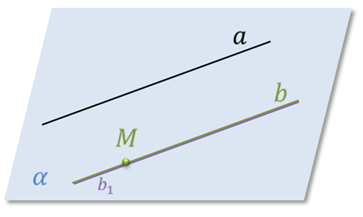
Рассмотрим прямую а и точку М, не лежащую на этой прямой. Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна. Тогда через нашу прямую а и точку М проходит единственная плоскость. Давайте обозначим эту плоскость буквой α. Прямая, проходящая через точку М параллельно прямой а, должна лежать в одной плоскости с точкой М и прямой а. Т.е. должна лежать в плоскости α. Из курса планиметрии вы помните, что через каждую точку плоскости, не лежащую на данной прямой, можно провести только одну прямую, параллельную данной прямой. Следовательно, в плоскости α через точку М проходит прямая, параллельная прямой а, и притом только одна. На рисунке эта прямая обозначена буквой b.
Докажем единственность прямой b. Предположим, что существует еще одна прямая, например, b1, которая проходит через точку М и параллельна прямой а. Тогда эта прямая b1 должна лежать в одной плоскости с точкой М и прямой а. Т.е. в плоскости α. А из курса планиметрии вы знаете, что в плоскости α через точку М проходит единственная прямая, параллельная прямой а. Значит, прямая b1 совпадает с прямой b.
Таким образом, прямая b – это единственная прямая, проходящая через точку М параллельно прямой а. Теорема доказана.
Замечание. Если прямые в пространстве параллельны, то на чертеже они обязательно изображаются параллельными прямыми.
А вот если прямые на чертеже изображены параллельными прямыми, то в пространстве эти прямые не обязательно параллельны.
Задание. Дан куб 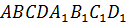 .
Параллельны ли прямые: а)
.
Параллельны ли прямые: а) 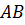 и
и 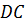 ;
б)
;
б) 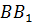 и
и 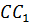 ;
в)
;
в) 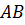 и
и 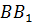 ;
г)
;
г) 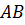 и
и 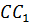 ?
?
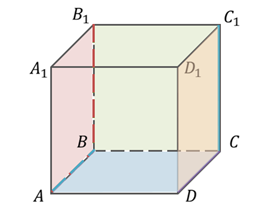
Решение. Рассмотрим куб ABCDA1B1C1D1. Напомню, что куб – это прямоугольный параллелепипед, все грани которого – равные квадраты.
Рассмотрим прямые AB и DC. Они лежат в одной плоскости ABC и не пересекаются. Следовательно, прямые AB и DC параллельны.
Аналогично и прямые BB1 и CC1. Они лежат в одной плоскости BB1C1 и не пересекаются. Следовательно, параллельны.
Теперь рассмотрим прямые AB и BB1. Хоть они и лежат в одной плоскости ABB1, но пересекаются в точке B. Значит, прямые AB и BB1 не параллельны.
Осталось рассмотреть прямые AB и CC1. Они не пересекаются, но и не лежат в одной плоскости. Значит, они не параллельны.
Ответ: а) 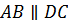 ;
б)
;
б) 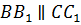 ;
в)
;
в) 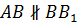 ;
г)
;
г) 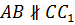 .
.
Подведем итоги урока. На этом уроке мы рассмотрели понятие параллельных прямых в пространстве. Узнали, что две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются. А также доказали теорему о том, что через любую точку пространства можно провести только одну прямую, параллельную данной.

 Получите свидетельство
Получите свидетельство Вход
Вход



 0
0 13908
13908

