Видеоучебник / Физика / Решение задач по основам МКТ, оптике и квантовой физике / Частные случаи уравнения состояния идеального газа

Новогодняя распродажа готовых материалов для учителей! Скидки до 50 %

Частные случаи уравнения состояния идеального газа

Урок 5. Решение задач по основам МКТ, оптике и квантовой физике

На этом уроке мы продолжим рассматривать решение задач с использованием уравнения состояния идеального газа, но уже с применением его к изопроцессам, т. е. к процессам, при которых один из макропараметров остается постоянным.

Плеер: YouTube Вконтакте

Конспект урока "Частные случаи уравнения состояния идеального газа"

Данная тема посвящена решению задач на частные случаи уравнения состояния идеального газа.

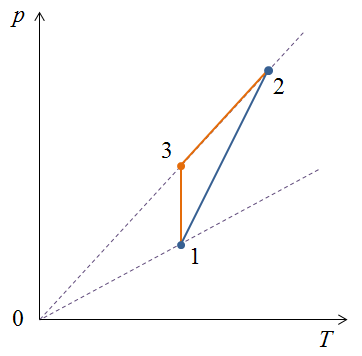
Задача 1. Идеальный газ постоянной массы переходит из состояния 1 в состояние 2 (см. рис.). Какой точке соответствует наибольший объем газа?

РЕШЕНИЕ

0 — 1: изохора;

0 — 2: изохора;

1 — 3: изотерма;

3 — 2: изохора.

Для изотермического процесса (1 — 3):

т.к. pV = const

Для изохорного процесса (3 — 2): V₃ = V₂

Ответ: наибольший объем газа соответствует точке 1.

Задача 2. В координатах p — V (см. рис.) представлен циклический процесс, происходящий с идеальным газом. Изобразите данный процесс в координатах p — T и V — T.

РЕШЕНИЕ

Рассмотрим представленный циклический процесс и проанализируем его. Из анализа процесса 1–2 следует, что процесс изохорный и

Из анализа процесса 2–3 можно заключить, что этот процесс изобарный и

В результате процесса 3–1 происходит уменьшение объема газа и увеличение его давления. Температура же газа, в этом случае, остается неизменной. Следовательно, процесс три-один — это изотермический процесс.

Теперь изобразим данный циклический процесс в координатах p–T.

Теперь построим график данного циклического процесса в координатных осях .

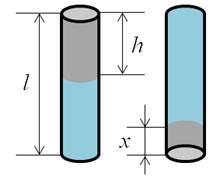
Задача 3. В вертикальной запаянной с одного конца стеклянной трубке, длина которой 70 см, находится столбик воздуха, запертый столбиком ртути высотой 20 см, доходящим до верхнего края трубки. Трубку медленно переворачивают, при этом часть ртути выливается, и высота столбика ртути, оставшейся в трубке, 35 мм. Определите атмосферное давление.

ДАНО:

СИ

РЕШЕНИЕ

Согласно условию задачи, воздух из трубки не выходит, значит его масса, входе процесса, остается неизменной. Также при медленном переворачивании трубки можно считать, что температура воздуха в трубке не изменяется. Поэтому, можно записать закон Бойля — Мариотта

в начальном состоянии воздух в трубке занимал объем, который, исходя из рисунка, можно определить, как

Давление воздуха в этом состоянии, согласно закону Паскаля, равно сумме внешнего (атмосферного) давления и гидростатического давления, оказываемого столбом ртути

В конечном состоянии объем воздуха определим, как

А давление воздуха в этом состоянии, согласно закону Паскаля, равно разности между внешним (атмосферным) давлением и гидростатическим давлением столба ртути высотой х

Тогда

Проверим размерности

Ответ: атмосферное давление составляет 101608 Па.

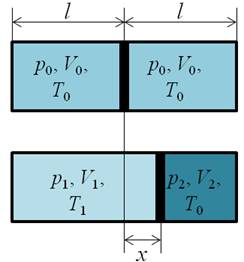
Задача 4. Закрытый с обоих концов цилиндр наполнен газом при давлении 1,01 ∙ 10⁵ Па и температуре 300 К и разделен легкоподвижным поршнем на две равные части длиной по 0,4 м каждая, причем давления и массы газа в обеих частях цилиндра одинаковы. На сколько градусов надо повысить температуру газа в одной части цилиндра, чтобы поршень сместился на 0,1 м, если во второй части цилиндра температура газа не изменяется. Определите давление газа после смещения поршня.

ДАНО:

РЕШЕНИЕ

Запишем уравнение состояния Менделеева-Клапейрона до нагревания газа

(1)

Уравнения Менделеева — Клапейрона после нагревания газа

(2)

(3)

Так как в конечном состоянии смещение поршня не происходит, то есть он находится в равновесии, то значение давления газа в левой части цилиндра равно давлению, которое оказывает газ в правой части цилиндра

Тогда

Определим давление газа после смещения поршня. Для этого сравним уравнения (1) и (3). Как видно в них равны правые части. Тогда

Рассмотрим второй способ решения.

При нагревании газа в одной его части изменяются все три параметра состояния. Поэтому основным уравнением, характеризующим данный процесс, служит уравнение объединенного газового закона

Процесс изменения состояния газа в другой части цилиндра — изотермический, поскольку по условию задачи там температура газа не изменяется. Поэтому для данного состояния газа применим закон Бойля — Мариотта

Тогда получаем

Ответ: ΔТ = 200 К; р = 1,35 ∙ 10⁵ Па.

Задача 5. Тонкостенный цилиндр высотой 0,2 м заполнен воздухом и закрыт сверху легкоподвижным невесомым поршнем. Цилиндр плавает на поверхности воды, наполовину погруженный в жидкость. Определите минимальную глубину, отсчитываемую от дна цилиндра, на которую можно погрузить цилиндр, чтобы он еще плавал. Атмосферное давление 10⁵ Па. Температура воды и воздуха одинаковы.

ДАНО:

РЕШЕНИЕ

В начальном состоянии на цилиндр действуют две силы — это сила тяжести воздуха, направленная вертикально вниз, и выталкивающая сила воды, направленная вертикально вверх