Связь между напряжением и напряжённостью. Эквипотенциальные поверхности

В 1839 году немецкий учёный Карл Фридрих Гаусс предложил изображать электростатические поля с помощью эквипотенциальных поверхностей.

Эквипотенциальной называется воображаемая поверхность, в каждой точке которой потенциал одинаков.

Из определения эквипотенциальной поверхности следует, что разность потенциалов между двумя любыми её точками равна нулю.

Давайте с вами вспомним, что разностью потенциалов называют скалярную физическую величину, численно равную отношению работы сил поля по перемещению заряда между данными точками поля к величине этого заряда:

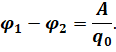
Из этого определения следует, что при переносе заряда вдоль эквипотенциальной поверхности работа полем не совершается (то есть она равна нулю).

Однако мы с вами знаем, что в общем случае работа сил электростатического поля пропорциональна переносимому заряду, модулю напряжённости поля, модулю перемещению и косинусу угла между направлением вектора электрической силы и вектора перемещения:

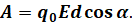
Но в записанной формуле значения заряда, модуля напряжённости и модуля перемещения всегда отличны от нуля. Поэтому должно равняться нулю значение косинуса угла альфа. А это значит, что угол альфа должен быть равен 90^о. Отсюда следует, что линии напряжённости электростатического поля всегда перпендикулярны эквипотенциальным поверхностям.

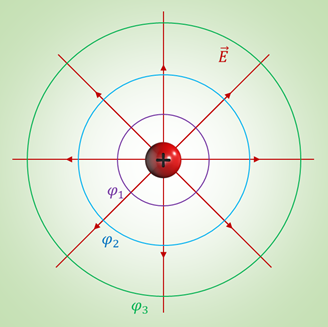
Так, например, эквипотенциальные поверхности однородного электростатического поля представляют собой плоскости, перпендикулярные линиям напряжённости. А эквипотенциальные поверхности точечного заряда — это сферы, в центре которых расположен заряд.

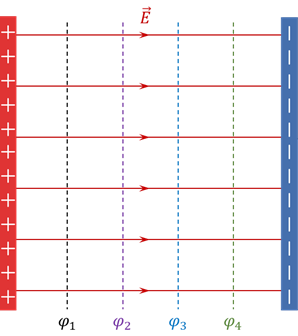
Зная картину эквипотенциальных поверхностей, можно определить напряжённость поля в любой его точке. Например, пусть заряд перемещается с одной эквипотенциальной поверхности на другую, расстояние между которыми по нормали равно d.

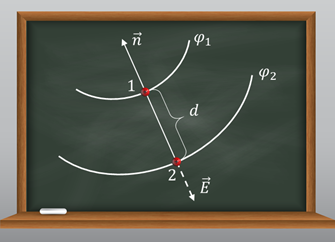
Мы уже знаем, что в этом случае работа, совершаемая электростатическим полем по перемещению заряда прямо пропорциональна величине этого заряда, напряжённости поля и модулю перемещения заряда:

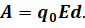
С другой стороны, работа поля по перемещению заряда из одной его точки в другую пропорциональна значению переносимого заряда и разности потенциалов начальной и конечной точек:

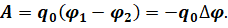
Давайте почленно разделим первое уравнение для работы на второе:

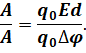
А из полученного выражения выразим модуль напряжённости поля:

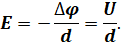
Полученная нами формула выражает связь между напряжённостью и разностью потенциалов (или напряжением) однородного электростатического поля. На её основании и вводится единица напряжённости в СИ — вольт на метр (В/м).

1 В/м — это модуль напряжённости такого однородного электростатического поля, в котором напряжение между двумя точками, лежащими на одной силовой линии на расстоянии 1 м, составляет 1 В.

В заключении отметим, что при изучении электростатического поля мы очень часто сравнивали его с гравитационным полем Земли.

В таблице представлены соответствия между механическими и электрическими величинами этих полей. Обсудите их со своим соседом (или соседкой) по парте.

А теперь, для закрепления материала, решим с вами несколько несложных задач. Задача 1. Напряжённость однородного электростатического поля, образованного двумя эквипотенциальными поверхностями, равна 10 кВ/м. Определите расстояние между этими поверхностями, если потенциал одной из них равен 200 В, а второй — – 150 В.

Задача 2. Между двумя разноимённо заряженными параллельными пластинами, находящимися на расстоянии 1 см друг от друга, покоится отрицательно заряженная капелька масла, плотность которого 900 кг/м³. Определите модуль заряда капельки, если её радиус равен 8 нм, а напряжение между пластинами составляет 650 В.