На прошлом уроке мы с вами говорили о том, что на помещённый в электростатическое поле пробный заряд, будет действовать сила, под действием которой заряд способен перемещаться вдоль линии напряжённости поля. Иными словами, электростатическое поле способно совершать работу, значение которой пропорционально величине переносимого заряда и зависит только от того, из какой и в какую точку поля заряд переносится:
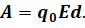
При этом на замкнутой траектории работа сил электростатического поля равна нулю.
Напомним, что если работа сил поля не зависит от формы траектории и на замкнутой траектории равна нулю, то такое поле называется потенциальными. Следовательно, точечный заряд, находящийся в любой точке электростатического поля, обладает потенциальной энергией взаимодействия с этим полем, значение которой определяют относительно произвольно выбираемой нулевой точки (чаще всего, это бесконечно удалённая точка поля). В нулевой точке потенциальную энергию заряда в поле принимают равной нулю. Тогда потенциальная энергия взаимодействия точечного заряда с электростатическим полем равна работе, которую совершили бы силы поля при перемещении данного заряда из указанной точки поля в нулевую точку:
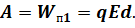
Из этого определения следует, что величина потенциальной энергии заряда в электростатическом поле пропорционально значению этого заряда:
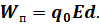
Иными словами, если мы будем вносить в одну и туже точку электростатического поля пробные заряды, значения которых будут отличаться в два, три, четыре и так далее раз, то потенциальные энергии этих зарядов будут отличаться во столько же раз.

Однако, отношение потенциальной энергии пробного заряда в поле к значению этого заряда для данной точки поля остаётся неизменным:

Отношение потенциальной энергии пробного заряда, помещённого в данную точку поля, к величине этого заряда, называется потенциалом электростатического поля в данной точке пространства:
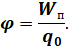
Обозначать потенциал мы будем греческой буквой «Фи» (φ).
Вы уже знаете, что силовой характеристикой электрического поля является напряжённость. Потенциал же характеризует энергетическое состояние поля в данной точке пространства.
Поскольку потенциальная энергия заряда в электростатическом поле зависит от выбора нулевой точки, то эта зависимость сохраняется и для потенциала. Если принять, что на бесконечно большом расстоянии от источника поле отсутствует, то потенциал поля в данной точке численно равен работе, совершаемой при перемещении пробного заряда из данной точки поля в бесконечность (то есть в нулевую точку):
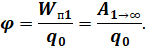
Найдём формулу, по которой можно рассчитать потенциал электростатического поля, создаваемого точечным зарядом, на некотором расстоянии от него. Для этого запишем формулу для определения работы электростатического поля:
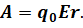
Здесь r — это расстояние от создающего поле заряда до исследуемой точки поля. А модуль напряжённости поля прямо пропорционален модулю этого заряда и обратно пропорционален квадрату расстояния между зарядом и точкой, в которой определяют значение напряжённости:
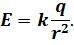
Перепишем формулу для потенциала поля с учётом наших рассуждений.
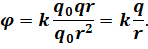
После упрощения, получим формулу, по которой можно рассчитать потенциал электростатического поля точечного заряда на заданном расстоянии от него. Из формулы видно, что знак заряда-источника поля определяет знак потенциала этого поля.
По этой же формуле можно рассчитывать и потенциал поля, создаваемого равномерно заряженной проводящей сферой в точках, находящихся вне сферы. Для точек же, находящихся на поверхности и внутри сферы, в знаменателе формулы «Эр малое» заменяется на радиус сферы:
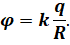
Если электростатическое поле создаётся системой зарядов, то имеет место принцип суперпозиции: потенциал такого поля в любой точке пространства равен алгебраической сумме потенциалов, создаваемых в этой точке каждым зарядом системы в отдельности:
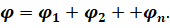
Зная потенциал поля в данной точке, можно рассчитать потенциальную энергию заряда, помещённого в эту точку:
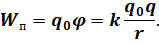
На прошлом уроке мы с вами отмечали тот факт, что работа сил электростатического поля по перемещению электрического заряда из начальной точки в конечную равна изменению потенциальной энергии, взятому с обратным знаком:
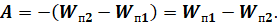
Давайте выразим потенциальную энергию через потенциалы поля в соответствующих точках:

Подставим значения потенциальных энергий в формулу для работы.
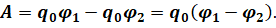
Как видно из полученной формулы, работа поля по перемещению заряда из одной его точки в другую пропорциональна значению переносимого заряда и разности потенциалов начальной и конечной точек.
А теперь давайте разделим выражение для работы на величину переносимого заряда q0:
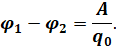
Скалярная физическая величина, численно равная отношению работы сил поля по перемещению заряда между данными точками поля к величине этого заряда, называется разностью потенциалов.
Как и изменение потенциальной энергии, разность потенциалов не зависит от выбора нулевой точки.
Из определения следует, что единицей разности потенциалов в СИ является Дж/Кл. Эта единица называется вольтом, в честь итальянского учёного Алессандро Джузеппе Антонио Анастасио Джероламо Умберто Вольта.
1 В — это разность потенциалов между двумя такими точками электростатического поля, при перемещении между которыми заряда в 1 Кл силами поля совершается работа 1 Дж.
Как вы, наверное, догадались, разность потенциалов очень часто называют напряжением.
То есть напряжение между двумя точками поля определяется работой сил этого поля по перемещению заряда 1 Кл из одной точки в другую. В электростатическом поле напряжение вдоль замкнутого контура всегда равно нулю.
Для закрепления нового материала, решим с вами несколько задач. Задача 1. В центре проводящей сферы с равномерно распределённым положительным зарядом в 45 нКл находится металлический шарик с отрицательным зарядом, модуль которого равен 17 нКл. Определите потенциал электростатического поля в точке, находящейся вне сферы на расстоянии 30 м от её центра.

Задача 2. Электрон влетает в однородное электростатическое поле по направлению силовой линии. Определите потенциал точки поля, в которой электрон поменяет направление движения, если в точке поля с потенциалом 1 В его скорость равнялась 300 км/с.


 Получите свидетельство
Получите свидетельство Вход
Вход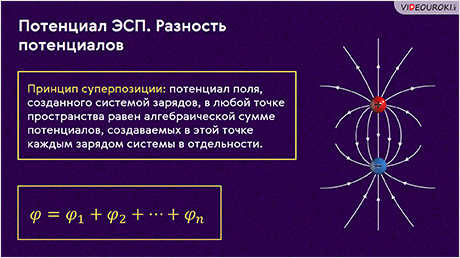



 1
1 17742
17742




Ребята ознакомьтесь с материалом видеоурока.