На прошлых уроках мы с вами говорили о том, что на помещённый в электростатическое поле пробный заряд действует кулоновская сила, под действием которой пробный заряд способен перемещаться вдоль линии напряжённости поля. Из механики мы знаем, что при перемещении тела действующая на него сила совершает работу. Логично предположить, что и электрическое поле также будет совершать работу по перемещению в нём заряда.
В общем случае работа сил электрического поля зависит как от начального и конечного положений перемещаемого заряда, так и от вида траектории, по которой он движется.
Однако электростатическое поле имеет важную особенность. Работа сил этого поля при перемещении заряда между двумя точками зависит только от положения этих точек и не зависит от вида траектории.
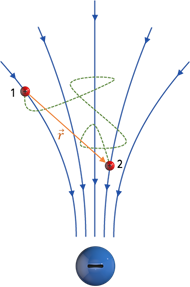
Давайте вспомним, что физические поля, работа сил которых не зависит от формы траектории, называют потенциальными (или консервативными). Покажем, что электростатическое поле потенциально.
Итак, пусть положительный пробный заряд находится в однородном электростатическом поле, созданном вертикальными параллельными пластинами, находящимися на расстоянии d друг от друга и имеющими заряды противоположных знаков.
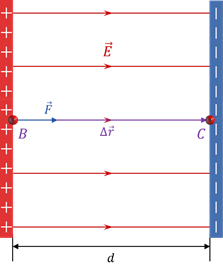
Предположим, что под действием электрической силы, действующей со стороны поля, заряд перемещается из точки В в точку С вдоль линии напряжённости рассматриваемого поля. При этом сила, с которой поле действует на пробный заряд, совершает работу.
Давайте вспомним, что в общем случае работа постоянной силы равна произведению модуля этой силы на модуль перемещения и на косинус угла между ними:
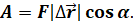
Модуль электрической силы мы найдём, как произведение величины пробного заряда и модуля напряжённости электростатического поля:
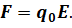
Так как направления силы и перемещения заряда совпадают, то косинус угла между нами равен единице:
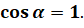
А модуль перемещения заряда равен расстоянию между точками В и С.
Тогда работа силы однородного электростатического поля по перемещению заряда прямо пропорциональна величине этого заряда, напряжённости поля и расстоянию, пройденному зарядом в поле под действием электрической силы:
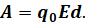
Теперь предположим, что заряд перемещается не вдоль силовой линии поля, а под некоторым углом к ней.
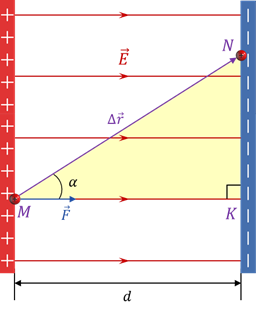
Обозначив угол между направлением вектора силы и вектора перемещения α, запишем формулу для работы поля в общем виде:
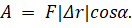
Для определения перемещения точки воспользуемся ΔMKN. Это прямоугольный треугольник, в котором гипотенуза — это искомое перемещение, а один из острых углов — это угол между вектором силы и вектором перемещения. Тогда очевидно, что произведение модуля вектора перемещения на косинус угла альфа равно длине прилежащего к углу катета М):
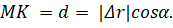
Следовательно, работа поля вновь равна произведению величины заряда, напряжённости поля и расстоянию, пройденному зарядом в поле под действием силы:
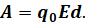
И, наконец, пусть перемещение нашего заряда из одной точки поля в другую происходит по криволинейной траектории.
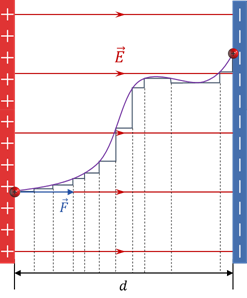
Чтобы найти работу поля, разобьём траекторию движения заряда на такие малые участки, что бы каждый из них можно было считать прямолинейным.Тогда работа на поля на всей траектории будет равна алгебраической сумме работ, совершаемых полем на каждом из маленьких участочков.
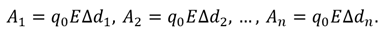
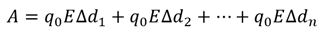
А теперь заметим, что в скобках стоит сумма длин прямолинейных участков, на которые мы разбили траекторию заряда. А это есть ни что иное, как расстояние между пластинами d. Таким образом мы получаем уже знакомую нам формулу:
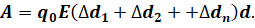
Таким образом действительно, работа силы однородного электростатического поля по перемещению заряда из одной точки поля в другую не зависит от формы траектории, по которой двигался пробный заряд, а зависит только от начального и конечного положений заряда.
Тогда становится очевидным, что в случае движения заряда по замкнутой траектории работа поля будет равна нулю, так как начальное и конечное положения заряда совпадают. Следовательно, однородное электростатическое поле потенциально. Это означает, что электростатическое и гравитационное поля имеют похожие свойства, определяемые их потенциальным характером.
Применительно к электростатическому полю эти свойства выражаются в следующем:
Во-первых, точечный электрический заряд, находящийся в любой точке электростатического поля, обладает потенциальной энергией взаимодействия с этим полем, значение которой определяют относительно произвольно выбираемой нулевой точки. В нулевой точке потенциальную энергию заряда в поле принимают равной нулю. Тогда потенциальная энергия взаимодействия точечного заряда с электростатическим полем равна работе, которую совершили бы силы поля при перемещении данного заряда из указанной точки поля в нулевую точку:
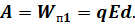
А во-вторых, работа сил электростатического поля по перемещению электрического заряда из начальной точки в конечную равна изменению потенциальной энергии, взятому с обратным знаком:
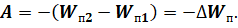
Знак «минус» в формуле означает, что если сила электростатического поля совершает положительную работу (подобно силе гравитационного поля Земли при падении мяча), то потенциальная энергия заряженного тела в поле уменьшается. Тогда, согласно закону сохранения энергии, кинетическая энергия заряженной частицы будет увеличиваться. На этом основано ускорение заряженных частиц электростатическим полем.
Если работа сил электростатического поля отрицательна (подобно работе силы гравитационного поля при движении мяча, брошенного вверх), то потенциальная энергия заряда в поле увеличивается, а кинетическая энергия наоборот уменьшается.
Обратим внимание ещё и на то, что потенциальная энергия — это энергия взаимодействия, и её необходимо относить не к заряженной частице или телу, а к системе в целом. В частности, для заряженной частицы, находящейся в электростатическом поле, это потенциальная энергия взаимодействия заряженной частицы с другими заряженными частицами или телами, являющимися источниками этого поля.

 Получите свидетельство
Получите свидетельство Вход
Вход





 7630
7630

