Здравствуйте, ребята!

Сегодня нам с вами предстоит непростая работа. Мы будем разбираться, как делить многозначные числа на двузначные числа второго десятка (11,12, 13, 14, 15, 16, 17, 18, 19). Число двадцать тоже входит во второй десяток, но деление на него мы рассматривать не будем. Ведь делить на двадцать – проще простого. Вы спросите, чем же такие числовые выражения отличаются от тех, значения которых мы находим уже не первый день?
А вот посмотрите. Сейчас я буду восемьсот двенадцать делить на четырнадцать так, как мы обычно это делаем.
Первое неполное делимое – восемьдесят один. В частном будет две цифры.
Восемьдесят один делим на четырнадцать. Делитель мы заменяем круглым числом. Восемьдесят один разделим на десять. Получается пробная цифра восемь. Перемножаем четырнадцать и восемь. Сто двенадцать. Ого, это при неполном делимом восемьдесят один! Восемь не подошло, пробуем цифру семь. Перемножаем четырнадцать и семь. Девяносто восемь. И семь тоже не подходит. Пробуем шесть. Четырнадцать умножаем на шесть – восемьдесят четыре. И снова мимо! Пробуем цифру пять. Перемножаем её с четырнадцатью, получается семьдесят. Ну наконец-то полученное произведение меньше неполного делимого. Но для того, чтобы удостовериться, что пробная цифра пять нам подходит, выполним вычитание. Остаток – одиннадцать. Он меньше делителя, значит, десятков в частном – пять. Следующее неполное делимое – сто двенадцать. Делим его на десять. Ничего себе! Получается одиннадцать. Но ведь мы ищем количество единиц в частном, и это должна быть одна цифра! Ни одиннадцать, ни десять нам не подходят. Возьмём в качестве пробной цифры девять. Перемножаем четырнадцать и девять. Сто двадцать шесть. Много! Возьмём восьмёрку. Сто двенадцать. Ну наконец-то! Восьмёрка подошла. Частное чисел восемьсот двенадцать и четырнадцать равно пятидесяти восьми.

Но согласитесь, такой долгий подбор – дело достаточно длительное и нудное. И так бывает довольно часто, если нужно делить на двузначное число второго десятка. А можно ли как-то ускорить процесс подбора цифр частного? Сейчас я поделюсь с вами своими маленькими секретами.
Во-первых, хочу напомнить вам, что если двузначный делитель оканчивается девяткой, то заменять его мы будем ближайшим к нему круглым числом. Поэтому при делении на девятнадцать для нахождения пробной цифры частного мы заменим девятнадцать не числом десять, а числом двадцать.
Допустим, пятьсот тринадцать разделим на девятнадцать.
Первое неполное делимое – пятьдесят один. В частном две цифры. Пятьдесят один делим не на десять, а на двадцать. Пробная цифра частного – два. Перемножаем её с девятнадцатью. Тридцать восемь. Вычитаем. Остаток – тринадцать. Всё получилось. Десятков в частном два. Второе неполное делимое – сто тридцать три. Делим на двадцать. Пробная цифра – шесть. Перемножаем её с девятнадцатью, получается сто четырнадцать. Вычитаем. Остаток – девятнадцать. Он равен делителю, значит шести в частном недостаточно. Берём семь. Умножаем на девятнадцать. Сто тридцать три. То, что надо. В частном семь единиц. И ответ: двадцать семь.
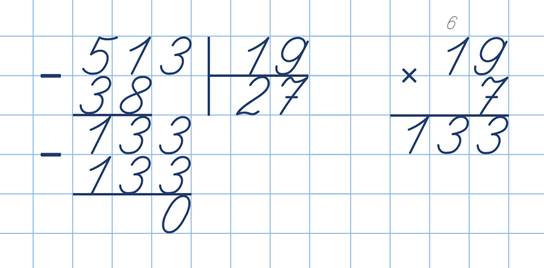
Как видите, в этом примере пробных цифр было не так много. Кстати, при делении на восемнадцать для нахождения пробной цифры можно заменить восемнадцать на двадцать.
Если делить придётся на одиннадцать, то, конечно, одиннадцать удобно заменить на ближайшее круглое число – десять. А вот как быть с числами от двенадцати до семнадцати?
А теперь я поделюсь с вами секретом подбора цифр в частном. Сейчас я буду делить девятьсот тридцать шесть на двенадцать.
Первое неполное делимое – девяносто три. В частном две цифры. Для подбора пробной цифры я делитель заменю не одним круглым числом, а двумя – десятью и двадцатью. Сначала девяносто три я разделю на двадцать. Получается четыре и остаток. Теперь это же неполное делимое разделю на десять. Получается девять и остаток. Между четырьмя и девятью на числовом луче находятся числа пять, шесть, семь и восемь. В качестве пробной цифры возьму ту, что находится посередине – шесть или семь.

Но так как двенадцать всё-таки ближе к круглому числу десять, то я возьму семёрку. Она ближе к пробной цифре девять, которая получилась при делении на десять. Перемножаю двенадцать и семь, получается восемьдесят четыре. Вычитаю его из неполного делимого. Остаток — девять. Прекрасно! Семь десятков в частном. Следующее неполное делимое – девяносто шесть. Оно немного больше первого неполного делимого, значит, пробная цифра может быть или тоже семёркой, или больше неё.

Если возьмём семь, то остаток будет двенадцать. Он равен делителю, что недопустимо. Берём пробную цифру восемь. Умножаем. Получилось девяносто шесть. Остаток – нуль, частное равно семидесяти восьми.
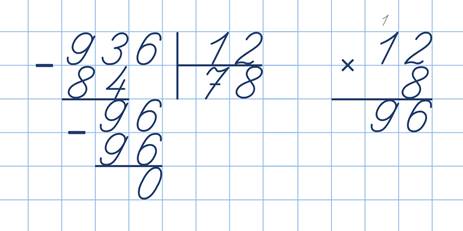
Как видите, пробных цифр не так уж и много.
Попробуем разделить пять тысяч девятьсот восемьдесят четыре на семнадцать.
Первое неполное делимое – пятьдесят девять. В частном три цифры.
Для подбора пробной цифры заменим семнадцать и на десять, и на двадцать. При делении на двадцать пробная цифра – два. При делении на десять – пять. Между цифрами два и пять на числовом луче находятся три и четыре. Так как число семнадцать ближе к двадцати, возьмём в качестве пробной тройку.

Умножаем на неё делитель, получается пятьдесят один. Вычитаем. Остаток – восемь. Он меньше делителя. Значит, количество сотен в частном мы нашли верно. Второе неполное делимое – восемьдесят восемь. При делении на двадцать получается пробная цифра четыре, а при делении на десять – восьмёрка. Между ними находятся цифры пять, шесть и семь. Беру ту, что посередине – шесть.

Перемножаю её с семнадцатью. Получилось сто два. Это много, шесть не подходит. Беру меньшую пробную цифру – пять. Перемножаю с семнадцатью, получается восемьдесят пять. Кажется, то, что надо. Вычитаю из восьмидесяти восьми. Остаток – три. В частном пять десятков. Следующее неполное делимое – тридцать четыре. При делении на двадцать – пробная цифра один, а при делении на десять – три. Между ними на числовом луче – двойка.

Берём её, перемножаем с семнадцатью, получается тридцать четыре, в частном две единицы и ответ триста пятьдесят два.
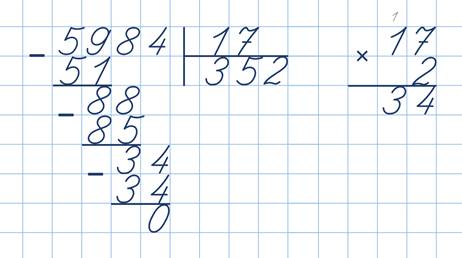
А теперь попробуйте сами найти значения таких числовых выражений, используя приём, о котором я сейчас вам рассказала:
544 : 16; 6678 : 13
Проверьте своё решение.

Ну а сейчас я покажу таблицу, которая также поможет вам быстрее выполнять вычисления, если необходимо разделить многозначное число на двузначное из второго десятка.
Вот эта таблица.
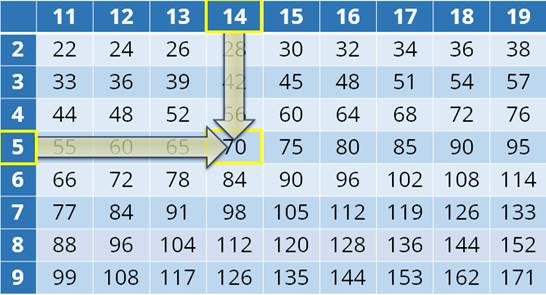
Она похожа на таблицу Пифагора. В верхнем ряду – двузначные числа от одиннадцати до девятнадцати, в первом столбике – однозначные числа от двух до девяти. А на пересечении вертикальной линии от какого-либо двузначного числа и горизонтальной от однозначного находится произведение этих двух чисел.
А теперь представьте себе, что нам надо разделить восемь тысяч шестьсот четыре на восемнадцать. Первое неполное делимое – восемьдесят шесть. В частном три цифры. Определяем количество сотен. Находим в таблице, в верхнем горизонтальном ряду делитель, восемнадцать, опускаемся вниз и находим числа, наиболее близкие числу восемьдесят шесть. Это семьдесят два и девяносто. Так как девяносто больше восьмидесяти шести, то оно нам не подходит.

Останавливаемся на числе семьдесят два и движемся по горизонтальной линии к однозначным числам. Приходим к числу четыре. Это и будет количество сотен. Проверяем. Перемножаем восемнадцать и четыре. Семьдесят два. Восемьдесят шесть минус семьдесят два – четырнадцать. Остаток меньше делителя. Всё верно. Следующее неполное делимое – сто сорок. Опять опускаемся от восемнадцати вниз. Самые близкие числа к числу сто сорок – это сто двадцать шесть и сто сорок четыре. То, что больше неполного делимого, нам не понадобится. Остаётся сто двадцать шесть. Идём по горизонтальной линии и приходим к числу семь.

Его и возьмём в качестве второй цифры частного, то есть количества десятков. Проверим это. Умножаем. Вычитаем. Остаток равен четырнадцати. Он меньше делителя. Продолжаем деление. Следующее неполное делимое – сто сорок четыре. Спускаемся от восемнадцати вниз.

Там есть число сто сорок четыре. Это – произведение чисел восемнадцать и восемь. Умножаем, вычитаем. Остаток – нуль. Частное равно четырёмстам семидесяти восьми.

Ну вот я и поделилась с вами своими секретами деления многозначных чисел на двузначные числа второго десятка. Надеюсь, они вам пригодятся.
А теперь нам пришло время прощаться. Успехов вам, ребята!

 Получите свидетельство
Получите свидетельство Вход
Вход
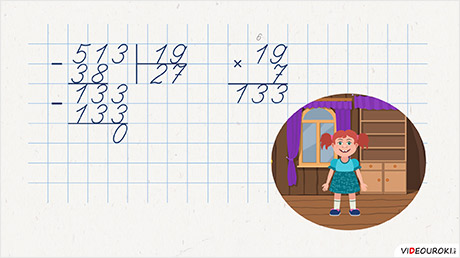



 0
0 3252
3252

