Метод координат. Разложение вектора по двум неколлинеарным векторам

Вопросы занятия:

·  повторить лемму о коллинеарных векторах;

·  поговорить о разложении вектора по двум неколлинеарным векторам.

Материал урока

Для начала необходимо вспомнить лемму о коллинеарных векторах.

Если векторы  и  коллинеарны и вектор , то существует такое число , что вектор .

Приведём доказательство этой леммы.

Для коллинеарных векторов  и  возможны два случая: векторы сонаправлены и векторы противоположно направлены.

Рассмотрим случай, когда векторы  и  сонаправлены.

Что и требовалось доказать.

Теперь рассмотрим случай противоположно направленных векторов  и .

Что и требовалось доказать.

Так мы доказали, что любой вектор  можно представить в виде произведения .

Задание.

Выразить коллинеарные векторы ,  и  через коллинеарный им вектор .

Решение.

А сейчас давайте повторим правило параллелограмма сложения двух векторов.

Если векторы-слагаемые  и  отложены от одной точки, то, построив на них параллелограмм , мы получим вектор  их суммы.

Обозначим вектор , как вектор . Он равен сумме векторов .

В свою очередь вектор , а вектор . Тогда можно записать, что вектор .

В таком случае говорят, что вектор  разложен по неколлинеарным векторам  и . Числа ,  при этом называют коэффициентами разложения.

Теорема.

На плоскости любой вектор можно разложить по двум данным неколлинеарным векторам, причём коэффициенты разложения определяются единственным образом.

Докажем это утверждение.

Пусть данными векторами будут неколлинеарные векторы  и . Докажем, что любой вектор  можно разложить по данным векторам.

Рассмотрим случай, когда вектор  коллинеарен одному из данных векторов, например, . В этом случае по лемме о двух коллинеарных векторах получаем, что вектор . Так же можно записать его разложение по векторам  и . Только коэффициент разложения при векторе  будет равен нулю.

Теперь рассмотрим случай, когда вектор . Отметим некоторую точку О и отложим от неё векторы ,  и , равные векторам ,  и  соответственно. Через точку P проведём прямую параллельную прямой OB. Точку пересечения полученной прямо с OA обозначим как А₁.

По правилу треугольника вектор . Вектор  коллинеарен вектору , вектор  коллинеарен вектору . Это значит, что вектор  можно представить в виде произведения , а вектор  — в виде произведения . Отсюда получаем, что вектор . Тем самым мы разложили его по векторам  и .

Первая часть теоремы доказана. Действительно, на плоскости любой вектор можно разложить по двум данным неколлинеарным векторам.

Теперь докажем, что коэффициенты разложения  и  определяются единственным способом.

Допустим, что кроме разложения  возможно другое разложение, например, .

Вычтем второе равенство из первого. Получаем,

Такое возможно только в том случае, если данные коэффициенты разложения равны

Значит, коэффициенты разложения определяются единственным способом.

Что и требовалось доказать.

Задание.

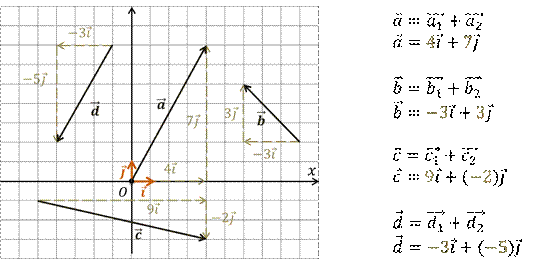
Разложить по двум векторам  и  векторы , ,  и , изображённые в координатной плоскости.

Решение.

Итоги урока

На этом уроке мы поговорили о «методе координат». Повторили лемму о коллинеарных векторах.  Поговорили о разложении вектора по двум неколлинеарным векторам.