В повседневной жизни мы часто встречается с понятием объема. На этом уроке мы поговорим об объеме тел. Выясним основные свойства объема.
Мы с вами начали изучать стереометрию. Напомню, что стереометрия – это раздел геометрии, в котором изучаются свойства фигур в пространстве. Как вы уже поняли, пространственные фигуры, или как их еще называют тела, в отличие от плоских фигур, обладают вместимостью, т.е. они имеют объем.
Такие фигуры называют объемными. Значит, мы с вами можем найти объем тела. А теперь давайте разберемся, как же мы будем его вычислять.
Из курса планиметрии вам известно понятие площади многоугольника. Напомню, что площадь – это величина части плоскости, которую занимает многоугольник. Или площадь – это положительная величина, определенная для каждого многоугольника, числовое значение которой обладает следующими свойствами:
1) равные многоугольники имеют равные площади;
2) если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников;
3) площадь квадрата, сторона которого равна единице измерения длины, равна единице.
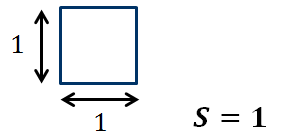
Каждый многоугольник имеет площадь, которая измеряется с помощью выбранной единицы измерения площадей. В качестве единицы измерения площадей обычно берут квадрат, сторона которого равна единице измерения отрезков.
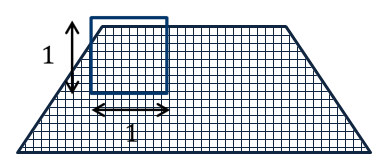
Площадь
может измеряться 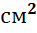 ,
,
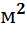 ,
, 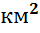 и т.д.
и т.д.
Процедура измерения объёмов аналогична процедуре измерения площадей. При выбранной единице измерения объём тела выражается положительным числом, которое показывает, сколько единиц измерения объёмов и её частей укладываются в этом теле.
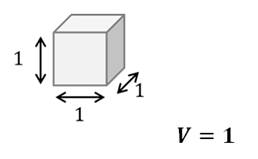
Чтобы измерить объем, надо выбрать единицу измерения объемов. Куб, ребро которого равно единице измерения длины, называется единичным. Объем единичного куба принимается за единицу измерения объемов.
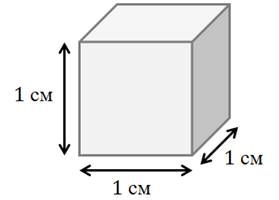
Например:
объем куба с ребром 1см равен одному кубическому сантиметру, пишут так: 1 куб.
см, или так 1 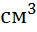 . Точно также
определяются и кубический миллиметр (1
. Точно также
определяются и кубический миллиметр (1 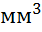 ),
кубический дециметр (1
),
кубический дециметр (1 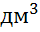 ),
кубический метр (1
),
кубический метр (1 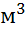 ),
кубический километр (1
),
кубический километр (1 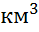 ).
).
Легко заметить, что название единицы объема получается из названия единицы длины присоединением прилагательного «кубический».
Измерить объем тела означает найти число, которое показывает, сколько единичных кубов содержится в этом теле.
Проще всего измерить объем прямоугольного параллелепипеда. Пусть у нас есть прямоугольный параллелепипед с измерениями: длина 5 см, ширина 3 см и высота 2 см.
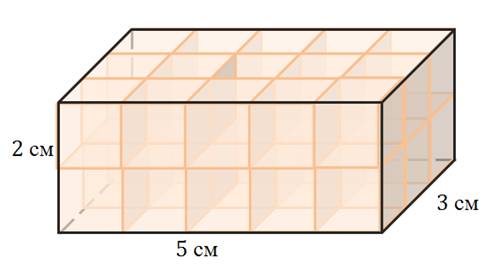
Посчитаем, сколько единичных кубов с ребром 1 сантиметр вмещается в нем.
Нижняя
грань параллелепипеда имеет длину 5 см и ширину 3 см. Поэтому, на ней можно
расположить 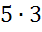 единичных кубов,
т.е. 15 единичных кубов.
единичных кубов,
т.е. 15 единичных кубов.
Чтобы
заполнить весь прямоугольный параллелепипед, нужно вложить 2 таких слоя, т.к.
высота параллелепипеда 2 см. Значит, всего таких кубов, которые вместятся в
этом параллелепипеде, будет равно 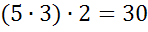 .
Следовательно, объем этого параллелепипеда
.
Следовательно, объем этого параллелепипеда 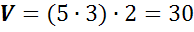 .
.
Напомню, что объем обозначается заглавной латинской буквой V.
Итак, объем – это положительная величина, определенная для каждого из рассматриваемых тел, числовое значение которой имеет следующие свойства:
1) равные геометрические тела имеют равные объемы;
2) если геометрическое тело составлено из нескольких тел, то его объем равен сумме объемов этих тел;
3) объем куба, ребро которого равно единице измерения длины, равен единице.
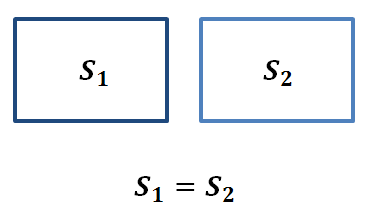
Рассмотрим первое свойство. Равенство двух фигур, в частности двух тел, в стереометрии определяется так же, как и в планиметрии: два тела называются равными, если их можно совместить наложением.
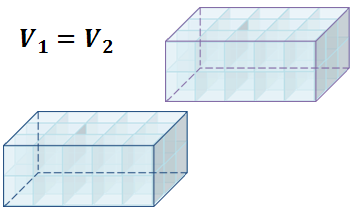
На рисунке изображены два равных прямоугольных параллелепипеда. Так как они равны, то каждый из них содержит столько же единиц измерения объемов, сколько и второй.
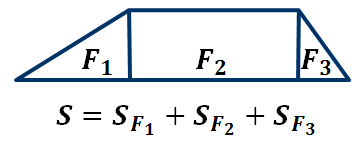
Рассмотрим второе свойство.
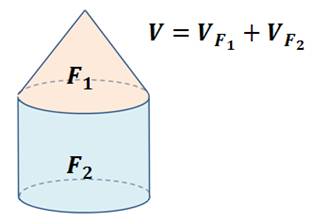
На рисунке изображено тело, составленное из нескольких тел, причем внутренние области этих тел не имеют общих точек. Понятно, что объем всего тела складывается из объемов составляющих его тел.
Первое и второе свойства называются основными свойствами объемов.
Для нахождения объемов тел часто удобно пользоваться теоремой, получившей название принцип Кавальери. Разберемся, в чем же состоит суть этого принципа. Рассмотрим два тела, заключенные между двумя параллельными плоскостями α1 и α2. Допустим, что любая плоскость, расположенная между плоскостями α1 и α2 и параллельная им, пересекает оба тела так, что площадь сечения первого тела в k раз больше площади сечения второго тела, причем число k – одно и то же для любой такой секущей плоскости. В этом случае, согласно принципу Кавальери, объем первого тела в k раз больше объема второго тела.
В практической деятельности человек часто встречается с необходимостью вычисления объемов, например при изготовлении каких-либо деталей, или при строительстве различных сооружений. Многие строительные объекты и детали конструкций имеют форму геометрических тел: параллелепипедов, призм, пирамид, шаров и т.д.
Подведем итоги урока. На этом уроке мы поговорили об объеме, одной из важных величин, связанной с геометрическими телами.
Итак, объем – это положительная величина, определенная для каждого из рассматриваемых тел, числовое значение которой имеет следующие свойства:
1) равные геометрические тела имеют равные объемы;
2) если геометрическое тело составлено из нескольких тел, то его объем равен сумме объемов этих тел;
3) объем куба, ребро которого равно единице измерения длины, равен 1.

 Получите свидетельство
Получите свидетельство Вход
Вход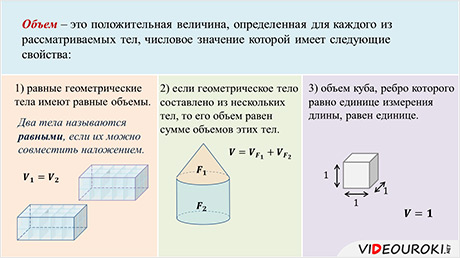



 0
0 6972
6972