На этом уроке мы дадим определение параллелепипеда. Назовем его элементы. А также рассмотрим свойства граней и диагоналей параллелепипеда.
Мы с вами начали изучать многогранники. Напомню, что многогранник представляет собой геометрическое тело, ограниченное конечным числом плоских многоугольников, любые два смежные из которых не лежат в одной плоскости.
Познакомились с призмой. n-угольной призмой называется многогранник, у которого две грани – равные n-угольники, а остальные n граней – параллелограммы.
Теперь давайте рассмотрим понятие параллелепипеда. Итак, параллелепипед – это четырехугольная призма, основаниями которой являются параллелограммы.
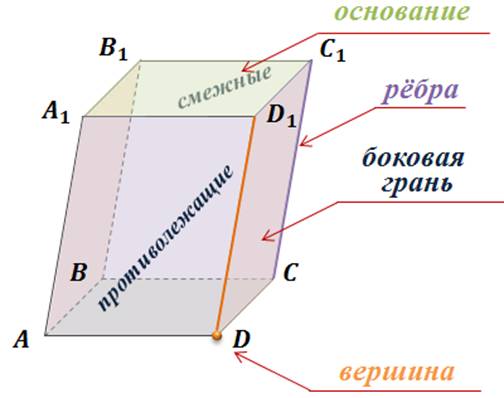
На рисунке изображен параллелепипед ABCDA1B1C1D1. Обратите внимание, все шесть граней параллелепипеда – параллелограммы.
Стороны параллелограммов называются ребрами параллелепипеда, а их вершины – вершинами параллелепипеда. Две грани параллелепипеда называются противолежащими, если они не имеют общего ребра. Например, грани AA1B1B и DD1C1C – противолежащие. Грани имеющие общее ребро называются смежными. Например, грани AA1D1D и DD1C1C – смежные, ребро DD1 у них общее.
Иногда какие-нибудь две противолежащие грани параллелепипеда выделяются и называются основаниями, тогда остальные грани – боковыми гранями, а их стороны, соединяющие вершины оснований параллелепипеда, - его боковыми ребрами. В нашем случае у параллелепипеда грани ABCD и A1B1C1D1 – его основания. Остальные же грани являются боковыми гранями.
Объединение боковых граней называется боковой поверхностью параллелепипеда, а объединение всех граней называется полной поверхностью параллелепипеда. Тогда площадью боковой поверхности параллелепипеда называется сумма площадей его боковых граней. А площадью полной поверхности параллелепипеда называется сумма площадей всех его граней.
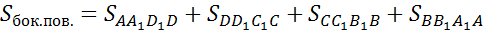
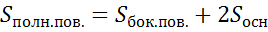
Если все боковые ребра параллелепипеда перпендикулярны к плоскостям его оснований, т. е. боковые грани – прямоугольники, то такой параллелепипед называется прямым. Если параллелепипед не является прямым, т.е. если все его боковые ребра не перпендикулярны к плоскостям оснований, то он называется наклонным. Если же и основаниями прямого параллелепипеда служат прямоугольники, то такой параллелепипед называется прямоугольным.
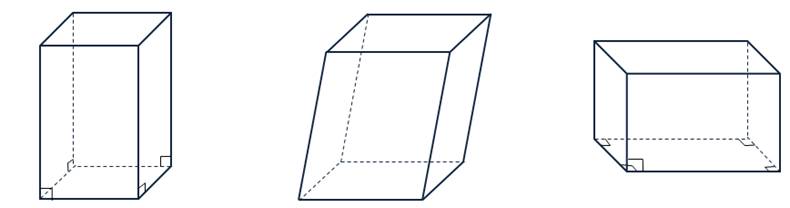
На рисунке вы видите примеры прямого, наклонного и прямоугольного параллелепипедов.
Представление о форме прямоугольного параллелепипеда дают спичечный коробок, коробка, холодильник и др. Обратите внимание, что всякий прямоугольный параллелепипед является прямым параллелепипедом, но не любой прямой параллелепипед есть прямоугольный. Основанием прямого параллелепипеда может служить параллелограмм, не являющийся прямоугольником. Представление о прямом, но не прямоугольном параллелепипеде дает, например, комната, в которой пол и потолок имеют форму ромба, не являющегося квадратом.
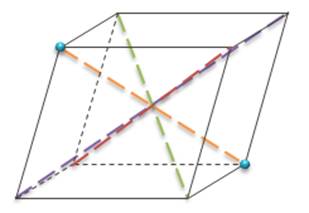
Две вершины параллелепипеда, не принадлежащие одной грани, называются противолежащими (обозначены точками). Отрезок, соединяющий, противолежащие вершины, называется диагональю параллелепипеда. У параллелепипеда всего четыре диагонали.
Куб – это прямоугольный параллелепипед, все ребра которого равны, т.е. все грани которого – равные квадраты.
Параллелепипед обладает следующими свойствами:
1) противолежащие грани параллелепипеда равны и лежат в параллельных плоскостях.
2) диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.
Докажем, что диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.
Доказательство этого утверждения основывается на следующем факте: если две прямые в пространстве параллельны третьей прямой, то они параллельны.
Мы знаем, что диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.
Если две прямые в пространстве параллельны третьей прямой, то они параллельны.
Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.
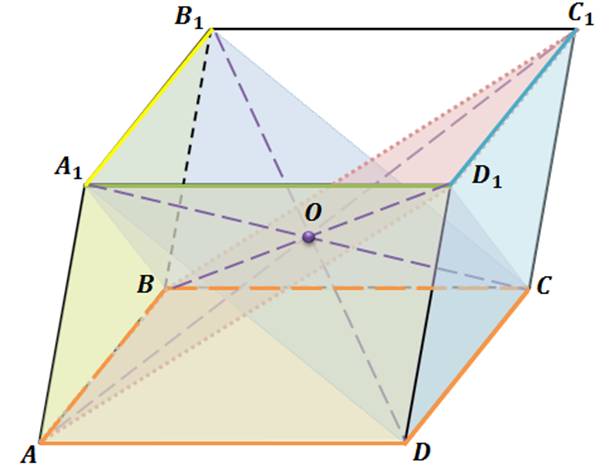
Итак, на рисунке изображен прямоугольный
параллелепипед  .
.
 ,
, 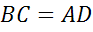 ,
, 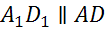 ,
, 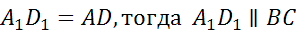 ,
, 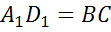
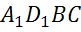 – параллелограмм
– параллелограмм 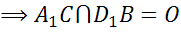
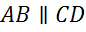 ,
, 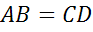 ,
, 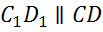 ,
, 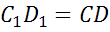 , тогда
, тогда 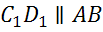 ,
, 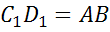
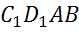 – параллелограмм
– параллелограмм 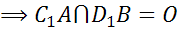
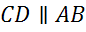 ,
, 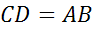 ,
, 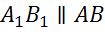 ,
, 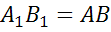 , тогда
, тогда 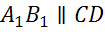 ,
, 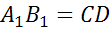
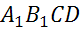 – параллелограмм
– параллелограмм 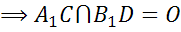
Таким образом, 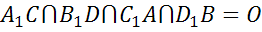
Что и требовалось доказать.
Задача. 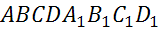 прямой параллелепипед,
основание
прямой параллелепипед,
основание 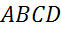 – квадрат. Найдите
площадь полной поверхности параллелепипеда, если ребро
– квадрат. Найдите
площадь полной поверхности параллелепипеда, если ребро 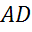 равно
равно 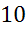 см, а ребро
см, а ребро 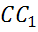 –
– 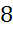 см.
см.
Решение.
По условию сказано, что наш параллелепипед прямой. Значит, все его боковые ребра перпендикулярны к плоскостям его оснований, т. е. боковые грани – прямоугольники. Т.к. в основании лежит квадрат, т.е. и основаниями прямого параллелепипеда служат прямоугольники, то наш параллелепипед прямоугольный. Из этого вытекает, что все боковые грани нашего параллелепипеда равные прямоугольники.
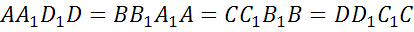
Напомню, что объединение всех граней называется полной поверхностью параллелепипеда. Тогда площадь полной поверхности параллелепипеда есть сумма площадей всех его граней.
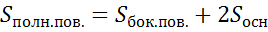
Для начала найдем площадь боковой поверхности. Она равна сумме площадей боковых граней параллелепипеда.
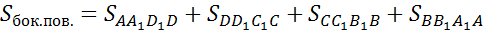
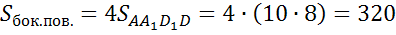 (см2)
(см2)
Теперь найдем площадь основания.
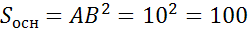 (см2)
(см2)
Подставим найденные площади в формулу. Посчитаем.
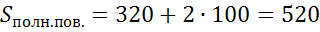 (см2)
(см2)
Ответ: 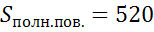 (см2).
(см2).
Подведем итоги урока.
На этом уроке мы рассмотрели параллелепипед. Узнали, что параллелепипед – это четырехугольная призма, основаниями которой являются параллелограммы. Назвали его элементы. А также рассмотрели свойства граней и диагоналей параллелепипеда.

 Получите свидетельство
Получите свидетельство Вход
Вход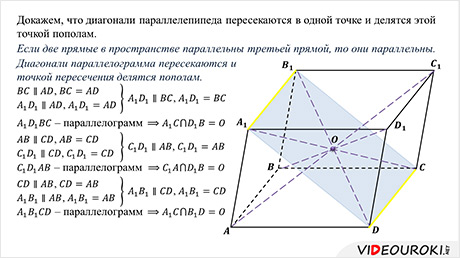



 0
0 6593
6593

