Ранее мы с вами уже познакомились с параллелепипедом. Напомню, что параллелепипед – это четырехугольная призма, основаниями которой являются параллелограммы.
Выяснили, что если все боковые ребра параллелепипеда перпендикулярны к плоскостям его оснований, т. е. боковые грани – прямоугольники, то такой параллелепипед называется прямым. Если параллелепипед не является прямым, т.е. если все его боковые ребра не перпендикулярны к плоскостям оснований, то он называется наклонным. Если же и основаниями прямого параллелепипеда служат прямоугольники, то такой параллелепипед называется прямоугольным.
А также узнали, что параллелепипед обладает следующими свойствами:
1) противолежащие грани параллелепипеда равны и лежат в параллельных плоскостях.
2) диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.
Сегодня мы подробней рассмотрим прямоугольный параллелепипед и выясним, какими свойствами он обладает.
Давайте представим себе комнату, имеющую форму прямоугольного параллелепипеда. Если говорить о ее размерах, то обычно употребляют слова «длина», «ширина» и «высота». Имея в виду длины трех ребер с общей вершиной. В геометрии эти три величины объединяются общим названием: измерения прямоугольного параллелепипеда.

На рисунке изображен прямоугольный параллелепипед ABCDA1B1C1D1.

В качестве его измерений можно взять, например, длины ребер DA, DC и DD1, все эти ребра имеют общую вершину D.
Как вы уже знаете у прямоугольника два измерения – длина и ширина.

При этом напомню,  .
.
Оказывается, что аналогичным свойством обладает и прямоугольный параллелепипед: квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.
Рассмотрим прямоугольный параллелепипед  . И
докажем, что
. И
докажем, что  –
диагональ параллелепипеда, а, b и c
– ребра, имеющие общую вершину.
–
диагональ параллелепипеда, а, b и c
– ребра, имеющие общую вершину.

Пусть  ,
,  ,
,  .
.
 ,
,

 –
прямоугольник.
–
прямоугольник.
Из  по
теореме Пифагора имеем
по
теореме Пифагора имеем  .
.
Из  по
теореме Пифагора имеем
по
теореме Пифагора имеем  .
.

Замечание. Данное утверждение называют пространственной теоремой Пифагора.
Рассмотрим еще одно свойство, иллюстрирующее аналогию между
прямоугольником и прямоугольным параллелепипедом. Мы знаем, что площадь
прямоугольника равна произведению его измерений. 
Оказывается, что аналогичное утверждение справедливо и для прямоугольного параллелепипеда: объем прямоугольного параллелепипеда равен произведению трех его измерений.
Для доказательства этого утверждения воспользуемся принципом Кавальери.
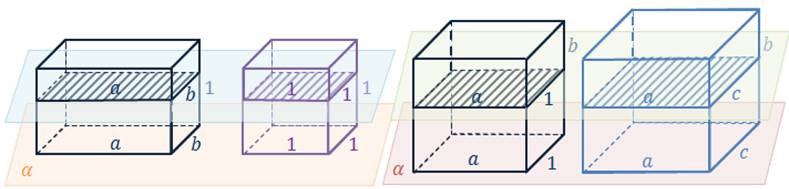
Рассмотрим сначала прямоугольный параллелепипед с измерениями а, b, 1 и куб с ребром 1, «стоящие» на плоскости α. Этот куб является единицей измерения объемов, т.е. его объем равен 1. Любая секущая плоскость, параллельная плоскости α, дает в качестве сечения куба квадрат площади равной 1, а в качестве сечения рассматриваемого параллелепипеда – прямоугольник площади равной произведению ab. Следовательно, согласно принципу Кавальери, объем этого параллелепипеда в а на b раз больше объема куба, т.е. равен ab.
Рассмотрим теперь два прямоугольных параллелепипеда: один с измерениями а, b, 1, а другой – с измерениями а, b, c, «стоящие» на плоскости α так, как показано на рисунке. Объем первого параллелепипеда, как было доказано, равен ab. Докажем, что объем второго параллелепипеда равен abc.
Любая секущая плоскость, параллельная плоскости α, дает в
качестве сечения первого параллелепипеда прямоугольник площади равной  , а в
качестве сечения второго – прямоугольник площади равной произведению
, а в
качестве сечения второго – прямоугольник площади равной произведению  .
Поэтому объем второго параллелепипеда в c раз больше
объема первого и, следовательно, равен
.
Поэтому объем второго параллелепипеда в c раз больше
объема первого и, следовательно, равен  . Что
и требовалось доказать.
. Что
и требовалось доказать.

В прямоугольном параллелепипеде с измерениями а, b,
c, изображенном на рисунке, площадь  , а
высота
, а
высота  .
Поэтому формулу
.
Поэтому формулу  можно записать в виде
можно записать в виде  ,
т.е. объем прямоугольного параллелепипеда равен произведению площади основания
на высоту.
,
т.е. объем прямоугольного параллелепипеда равен произведению площади основания
на высоту.
Оказывается, что такая же формула имеет место для любой призмы: объем призмы равен произведению площади основания на высоту.
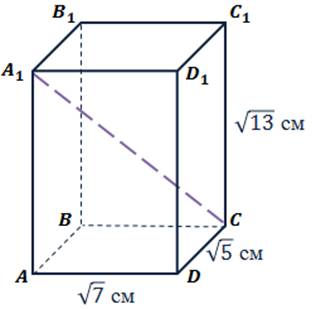
Задача.  прямоугольный
параллелепипед. Определите чему равна диагональ
прямоугольный
параллелепипед. Определите чему равна диагональ  ,
если параллелепипед имеет измерения
,
если параллелепипед имеет измерения  см,
см,
 см
и
см
и  см.
см.
Решение.
Напомню, что квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.


 (см)
(см)
Ответ:  (см).
(см).
Задача.  прямоугольный
параллелепипед, основание
прямоугольный
параллелепипед, основание  –
квадрат. Объем
–
квадрат. Объем  см3.
Определите высоту прямоугольного параллелепипеда, если
см3.
Определите высоту прямоугольного параллелепипеда, если  см.
см.
Решение.
На этом уроке мы доказали, что объем прямоугольного параллелепипеда равен произведению площади основания на высоту. Выразим из формулы высоту.


 (см2)
(см2)
 (см)
(см)
Ответ:  (см).
(см).
Подведем итоги урока. На этом уроке мы подробно рассмотрели прямоугольный параллелепипед. И выяснили, что прямоугольный параллелепипед обладает свойствами, иллюстрирующими аналогию с прямоугольником. А именно квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений. И объем прямоугольного параллелепипеда равен произведению трех его измерений. А также объем прямоугольного параллелепипеда можно вычислить как произведение площади основания на высоту.

 Получите свидетельство
Получите свидетельство Вход
Вход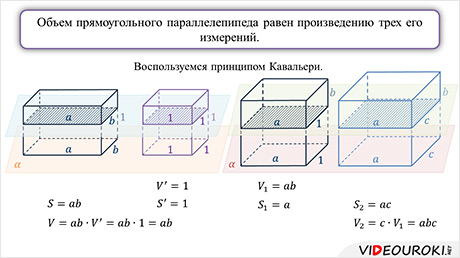



 0
0 22553
22553

