На этом уроке мы познакомимся с понятием пирамиды. Дадим определение пирамиды. Рассмотрим, какими элементами она обладает. Узнаем, какую пирамиду называют правильной, и какими свойствами она обладает. А также разберемся, как находят объем пирамиды.
Мы с вами начали изучать многогранники. Напомню, что многогранник представляет собой геометрическое тело, ограниченное конечным числом плоских многоугольников, любые два смежные из которых не лежат в одной плоскости.
Теперь давайте рассмотрим понятие пирамиды. Пирамида – это один из видов многогранника. Можно привести много примеров пирамиды из реальной жизни. Наверняка каждый из вас в детстве собирал игрушечную пирамидку, на уроках истории вас знакомили со знаменитыми египетскими пирамидами, многие известные архитектурные строения имеют форму пирамиды. Это и башни Кремля, пирамида Лувра, станция метро в Мюнхене и так далее.

Итак, рассмотрим многоугольник ![]() и точку P, не лежащую в плоскости этого многоугольника. Соединим
точку P отрезками с вершинами многоугольника. В
итоге получим n треугольников:
и точку P, не лежащую в плоскости этого многоугольника. Соединим
точку P отрезками с вершинами многоугольника. В
итоге получим n треугольников: ![]() ,
,
![]() , … ,
, … , ![]() . Многогранник,
составленный из n -угольника
. Многогранник,
составленный из n -угольника ![]() и этих n треугольников, называется пирамидой.
и этих n треугольников, называется пирамидой.
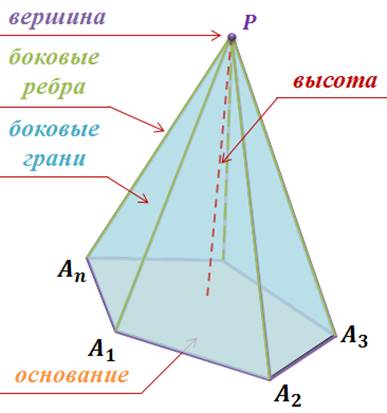
Многоугольник ![]() называется
основанием пирамиды. Треугольники
называется
основанием пирамиды. Треугольники ![]() ,
, ![]() , … ,
, … , ![]() называются
боковыми гранями пирамиды. Точка P – вершиной пирамиды, а отрезки PA1,
PA2…PAn –
ее боковыми ребрами.
называются
боковыми гранями пирамиды. Точка P – вершиной пирамиды, а отрезки PA1,
PA2…PAn –
ее боковыми ребрами.
Пирамиду с вершиной P и
основанием ![]() называют n-угольной
пирамидой и обозначают так:
называют n-угольной
пирамидой и обозначают так: ![]() .
.
Отрезок, соединяющий вершину пирамиды с плоскостью ее основания и перпендикулярный к этой плоскости, называется высотой пирамиды.
Объединение боковых граней называется боковой поверхностью пирамиды, а объединение всех граней называется полной поверхностью пирамиды. Тогда площадью боковой поверхности пирамиды называется сумма площадей ее боковых граней. А площадью полной поверхности пирамиды называется сумма площадей всех ее граней.
![]()
![]()
Пирамида в зависимости от того какой многоугольник лежит в основании имеет свое название. Если в основании лежит треугольник, то пирамида называется треугольной. Если четырехугольник – то четырехугольной пирамидой. А если n-угольник, то n-угольной пирамидой.

Пирамида называется правильной, если ее основание – правильный многоугольник, а отрезок, соединяющий вершину пирамиды с центром основания, является ее высотой. Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой.

На рисунке изображена правильная пирамида. PE – одна из ее апофем. Все апофемы правильной пирамиды равны друг другу.
Отметим некоторые свойства правильной n-угольной пирамиды.
1. В правильной -угольной пирамиде все боковые ребра равны между собой.
![]()
2. Из равенства боковых ребер пирамиды следует и равенство ее боковых граней.
![]()
Рассмотрим куб со стороной а и проведем его диагонали.

Обратите внимание, в результате куб окажется разбитым
на 6 равных друг другу правильных пирамид с общей вершиной в точке пересечения
диагоналей куба. У каждой из этих пирамид основанием является квадрат со
стороной а, высота ![]() , а объем в 6 раз меньше объема
куба, т.е. равен
, а объем в 6 раз меньше объема
куба, т.е. равен ![]() . Но в свою очередь,
. Но в свою очередь, ![]() можно
расписать как
можно
расписать как ![]() – ее высота. Таким
образом, объем правильной четырехугольной пирамиды со стороной основания а и
высотой h равен
– ее высота. Таким
образом, объем правильной четырехугольной пирамиды со стороной основания а и
высотой h равен ![]() .
.
Полагаясь на этот факт, можно доказать, что
аналогичное утверждение справедливо и для произвольной пирамиды: ![]() .
.
Задача. ![]() –
правильная пирамида. Найдите площадь боковой поверхности, если
–
правильная пирамида. Найдите площадь боковой поверхности, если ![]() см, а
см, а ![]() см.
см.
Решение: напомню, что площадью боковой поверхности пирамиды называется сумма площадей ее боковых граней.
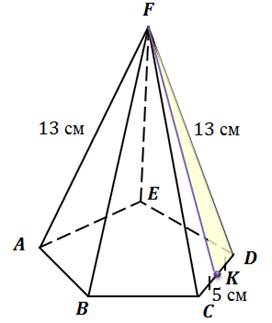
Т.к. по условию задачи сказано, что FABCDE
– правильная пирамида, то в ее основании лежит правильный пятиугольник и все ее
боковые ребра равны между собой. Следовательно, ![]()
![]() см
см
![]()
![]() – высота, медиана
и биссектриса.
– высота, медиана
и биссектриса.
![]() – прямоугольный.
– прямоугольный.
![]()
![]()
![]() (см)
(см)
![]()
![]() (см2)
(см2)
Ответ: ![]() .
.
Интересно знать! Пирамиды – величайшие строения мира, которые завораживают и привлекают внимание людей. О различных свойствах пирамиды слагают легенды. Существуют даже научно доказанные факты о волшебных свойствах пирамиды.
В древние времена к числу «семи чудес света» относилась и египетская Великая пирамида.
Она была построена примерно 4600 лет назад для фараона Хуфу (его еще называли Хеопсом) и стала крупнейшей из трех пирамид, которые до сих пор возвышаются в районе города Гиза. Для ее строительства потребовалось вытесать и доставить на место примерно 2 300 000 каменных блоков общим весом почти 6 миллионов тонн. Внутри пирамиды есть несколько проходов и камер. Каждая боковая грань пирамиды имеет форму треугольника, а основанием служит квадрат со стороной 230 метров. Высота пирамиды – 147 метров, что соответствует современному пятиэтажному зданию.
Подведем итоги урока. На этом уроке мы познакомились с понятием пирамиды. Узнали, что многогранник, составленный из n-угольника A1A2…An и n треугольников, называется пирамидой. Рассмотрели, из каких элементов она состоит. Узнали, какую пирамиду называют правильной, и какими свойствами она обладает. А также разобрались, как находят объем пирамиды.

 Получите свидетельство
Получите свидетельство Вход
Вход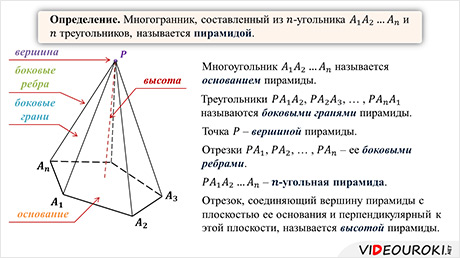



 0
0 5090
5090

