Применение производной для отыскания точек экстремума

Вопросы занятия:

·     рассмотреть нахождение точек экстремума с помощью производных.

Материал урока.

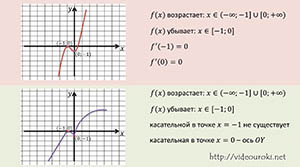
Пусть график функции f(x) имеет вид:

Легко заметить, что

Давайте посмотрим на точки (-1; 0) и (0; -1) подробнее. В этих точках происходит изменение характера монотонности функции (слева от точки (-1; 0) функция возрастает, а справа от неё до точки (0; -1) – убывает. Слева от точки (0; -1) функция убывает, а справа – возрастает. Касательные к графику функции в этих точках параллельны оси Ox, то есть можно записать, что производная функции в этих точках равна нулю.

Если рассмотреть некоторую окрестность точки x = -1, то легко заметить, что f(-1) – это наибольшее значение функции в этой окрестности.

Теперь давайте рассмотрим ещё один график функции.

Чем-то он похож на предыдущий график. В точках (-1;0), (0; -1) также происходит смена характера монотонности, но в точке x = -1 касательной к графику не существует, а в точке x = 0 касательная перпендикулярна оси Ox, то есть совпадает с осью Oy.

Если рассмотреть некоторую окрестность точки x = -1, то легко заметить, что f (-1) – это наибольшее значение функции в этой окрестности.

Если же мы рассмотрим некоторую окрестность точки x = 0, то увидим, что f(0) – это наименьшее значение в этой окрестности.

Определение.

Точку x = x₁ называют точкой минимума функции y = f(x), если у этой точки существует окрестность, для всех точек которой выполняется неравенство f (x) ≥ f(x₀).

Функции, графики которых мы построили, имеют точку минимума

x = 0. Потому что можно выбрать окрестность, например, (-1/2; ½) или (-0,2; 0,2), для всех точек которой выполняется неравенство f(x) ≥ f (0).

Значение функции в точке минимума обозначают y_min. Не будем путать это значение с наименьшим значением функции. Очевидно, что функции, графики которых изображены на рисунках, не имеют наименьших значений. А y_min существуют.

Определение.

Точку x = x₁ называют точкой максимума функции y = f(x), если у этой точки существует окрестность, для всех точек которой выполняется неравенство f (x) ≤ f(x₀).

Функции, графики которых мы построили, имеют точку максимума

x = -1. Потому что можно выбрать окрестность, например, (-3/2; -1/2), для всех точек которой выполняется неравенство f (x) ≤ f (-1). Это верно для обеих функций.

Значение функции в точке максимума обычно обозначают y_max. Не будем путать это значение с наибольшим значением функции. Очевидно, что функции, графики которых изображены на рисунках, не имеют наибольших значений. А y_max существует.

Точки минимума и максимума функции объединяют общим термином – точки экстремума (от латинского слова экстремум, что означает крайний).

В математике исследование задач на максимум и минимум началось очень давно – двадцать пять веков назад, Долгое время к задачам на отыскание экстремумов не было сколько-нибудь единых подходов. Но примерно триста лет назад – в эпоху формирования математического анализа – были созданы первые общие методы решения и исследования задач на экстремум.

Большую работу в этом направлении проводили Ферма и Эйлер. Правила определения экстремумов функции одной переменной y = f (x) были даны Маклореном.

Если функция y = f (x) достигает в точке x₀ минимума или максимума, то название точка минимума или максимума используют как для значения x = x₀ так и для точки (x₀; f (x₀)).

Теперь давайте посмотрим, как же искать точки экстремума. Посмотрим на наши графики ещё раз.

На первом графике в обеих точках экстремума производная обращается в ноль. А для функции, график которой изображён на втором рисунке в обеих точках экстремума производная не существует.

Сформулируем теорему. Поскольку наша тема неразрывно связана с темой об определении промежутков монотонности, то мы продолжим нумерацию теорем.

Теорема 4.

Если функция y = f (x) имеет экстремум в точке x = x₀, то в этой точке производная функции либо равна нулю, либо не существует.

Внутренние точки области определения, в которых производная функции равна нулю, называют стационарными, а внутренние точки области определения, в которых функция непрерывна, но производная не существует, называют критическими.

Возникает вопрос: верно ли обратное утверждение, то есть верно ли, что если x = x₀ – это стационарная или критическая точка, то в этой точке функция имеет экстремум? Нет. Это утверждение неверно. Например, построим график некоторой функции.

Легко заметить, что у данной функции существует и стационарная и критическая точки, но также легко заметить, что ни одна из этих точек не является эктремумом функции. То есть нельзя подобрать таких окрестностей этих точек, в которых бы значения в этих точках были наибольшим или наименьшим значением.

Таким образом, четвертая теорема даёт только необходимое условие экстремума, но оно не является достаточным.

А как же узнать, есть ли в стационарной или в критической точке экстремум?

Ещё раз посмотрим на наши графики.

Обратим внимание, что при переходе через точку максимума меняется характер монотонности (слева от точки максимума функция возрастает, справа – убывает). Соответственно изменяются знаки производной: слева от точки максимума производная положительна, справа – отрицательна.

Если же и слева и справа от стационарной или критической точки производная имеет один и тот же знак, то в этой точке экстремума нет.

Именно так и получается на последнем рисунке. И слева и справа от стационарной и критической точек производная положительна.

Эти рассуждения могут служить подтверждением справедливости следующей теоремы.

Теорема 5. Пусть функция y = f (x) непрерывна на промежутке X и имеет внутри промежутка стационарную или критическую точку x =x₀. Тогда: если у этой точки существует такая окрестность, в которой при x < x₀ выполняется неравенство f'(x) < 0, а при x > x₀ – выполняется неравенство f'(x) > 0, то x =x₀ – это точка минимума функции y = f (x); если у этой точки существует такая окрестность, в которой при x < x₀ выполняется неравенство f'(x) > 0, а при x > x₀ – выполняется неравенство f'(x) < 0, то x =x₀ – это точка максимума функции y = f (x); если у этой точки существует такая окрестность, что в ней и слева и справа от точки x₀ знаки производной одинаковы, то в точке x₀ экстремума нет.

На практике удобнее применять условную схему для знаков производной.

Рассмотрим пример.

Пример.

На этом примере мы увидели, что монотонность и экстремумы тесно связаны между собой. Поэтому можно составить общий алгоритм исследования непрерывной функции y = f (x) на монотонность и экстремумы.

Рассмотрим это на примере.

Пример.

Рассмотрим ещё один пример.

Пример.