Параллельные прямые

Две прямые на плоскости могут либо пересекаться, либо не пересекаться.

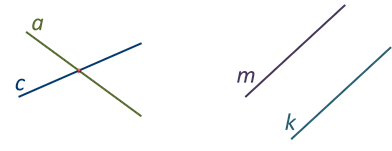
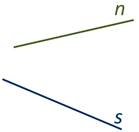
Даже если на рисунке мы не видим точку пересечения прямых n и s, это не значит, что они не пересекаются вовсе. Помните, что прямые можно бесконечно продлевать в обе стороны.

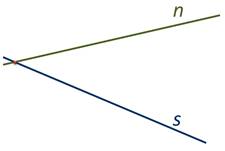
А значит, продлив прямые, мы найдём точку пересечения прямых.

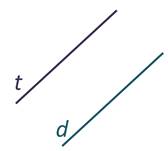
А вот прямые t и d не пересекутся никогда.

Такие прямые называют параллельными.

Определение

Таким образом, две непересекающиеся прямые на плоскости называются параллельными.

На рисунке прямая t параллельна прямой d.

В математике слово “параллельные” обозначают специальным символом:

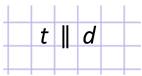
В математике вы уже не раз встречались с параллельными прямыми.

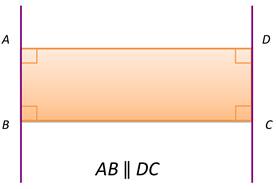
Например, если продлить противоположные стороны прямоугольника, то полученные прямые будут параллельны.

Кроме того, представление о параллельных прямых мы можем получить, если посмотрим на железнодорожные рельсы или на электрические провода.

Убедиться в том, что две прямые параллельны можно с помощью чертёжного треугольника и линейки.

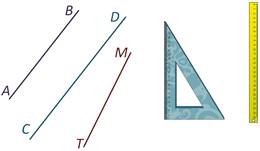
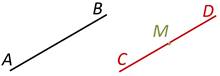
Давайте определим, параллельна ли прямая АВ прямой СD, параллельна ли прямая АВ прямой МТ. Для этого берём чертёжный треугольник и совмещаем сторону прямого угла чертёжного треугольника с прямой АВ. К другой стороне угольника прикладываем линейку.

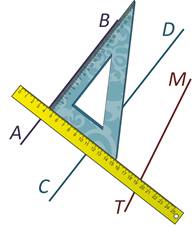
Теперь двигаем угольник вдоль линейки до прямой СD.

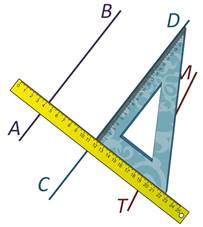
Прямая АВ параллельна прямой СD.

Двигаемся до прямой МТ.

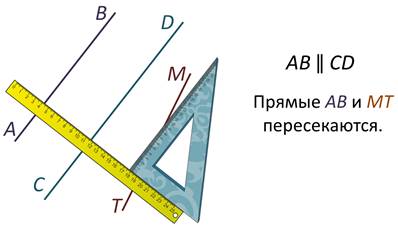
Прямая АВ не параллельна прямой МТ.

Построить параллельные прямые не сложно.

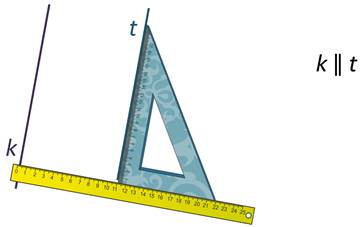
Для построения прямой линии, параллельной прямой k, надо приложить угольник к прямой k, к другой стороне угольника прикладываем линейку. Теперь двигаем угольник вдоль линейки. Проводим прямую t вдоль другой стороны угольника.

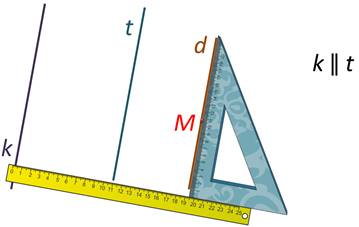
Если нам нужно провести прямую через определённую точку, мы будем действовать так же: прикладываем угольник и линейку; затем, передвигая угольник вдоль линейки, добьёмся того, чтобы точка М оказалась на стороне угольника; теперь проведём прямую d.

Построение параллельных прямых закончено.

Обратите внимание, что через каждую точку плоскости, не лежащую на данной прямой, можно провести только одну прямую, параллельную данной прямой.

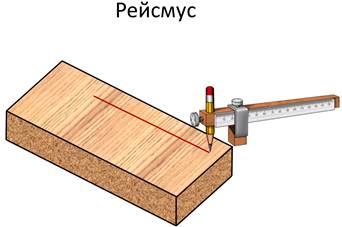
Кстати, прибор, которым пользуются плотник и столяр для построения линии параллельной краю доски называется рейсмус.

Вернёмся к чертежу, на котором мы строили параллельные прямые.

Посмотрите внимательно на рисунок: прямая t параллельна прямой k. Кроме того, прямая d параллельна прямой k. Не сложно убедиться, что прямые t и d тоже параллельны.

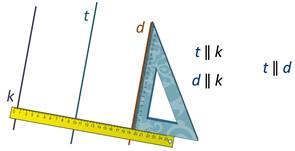
То есть, если две прямые на плоскости параллельны третьей прямой, то они параллельны.

При построении параллельных прямых, мы использовали угольник. Напомню, с помощью угольника можно легко строить перпендикулярные прямые. То есть прямые, которые при пересечении образуют угол 90^о.

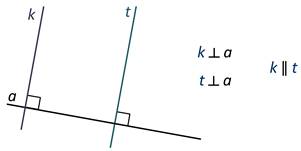
А это значит, что если вдоль другой стороны угольника провести прямую а, то эта прямая будет перпендикулярна прямой k. Кроме того, прямая t будет перпендикулярна прямой а.

А сами прямые k и t параллельны.

То есть, если две прямые на плоскости перпендикулярны третьей прямой, то они параллельны.

Например, если продлить смежные (то есть соседние) стороны прямоугольника, то полученные прямые будут перпендикулярны.

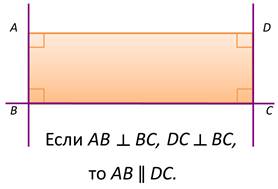
А значит, противоположные стороны прямоугольника будут параллельны.

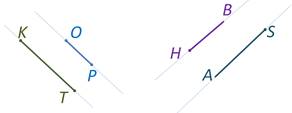
Кроме параллельных прямых в математике есть понятие «параллельные отрезки (или лучи)».

Определение

Отрезки (или лучи), лежащие на параллельных прямых называются параллельными.

Например, отрезки KT и OP параллельны, т.к. через них можно провести параллельными прямые. Лучи SA и HB лежат на параллельных прямых, а значит параллельны.

Приведём примеры параллельных прямых в окружающей обстановке.

Посмотрите внимательно, противоположные стороны картины параллельны. Кроме того, параллельные отрезки можно найти и на двери, и на окне, и даже на обоях.

Итоги

Две непересекающиеся прямые на плоскости называются параллельными.

Если две прямые на плоскости параллельны третьей прямой, то они параллельны.

Если две прямые на плоскости перпендикулярны третьей прямой, то они параллельны.

Через каждую точку плоскости, не лежащую на данной прямой, можно провести только одну прямую, параллельную данной прямой.