Представим себе такую историю…
– Паша, что ты читаешь? – спросил у друга Саша.
– Я читаю книгу о поездах, – ответил другу Паша. – В ней очень много интересного написано. Например, я узнал, когда появились первые поезда и как они были устроены, когда и где появилась первая железная дорога.
– Знаешь, Паша, мне всегда было интересно, как расположены железнодорожные рельсы, – сказал Саша.
– В книге написано, что рельсы можно сравнить с параллельными прямыми, – рассказал Паша.

– А что это за параллельные прямые? – спросил Саша.
– Даже не знаю, – ответил Паша. – А давай спросим у Мудряша.
– Ребята, прежде чем мы с вами поговорим, давайте немного разомнёмся и выполним устные задания, – предложил Мудряш.
– Теперь сверимся! – сказал Мудряш. – Посмотрите, что у вас должно было получиться!

–
А сейчас вернёмся к вашему вопросу, – начал Мудряш. – Ребята, давайте
разберёмся, какие же прямые называют параллельными. Пусть на плоскости есть
прямая 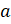 и
точка
и
точка 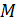 , которая не лежит
на этой прямой.
, которая не лежит
на этой прямой.
Проведём
через точку 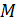 несколько прямых.
Обратите внимание, каждая из этих прямых, кроме прямой
несколько прямых.
Обратите внимание, каждая из этих прямых, кроме прямой 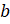 , пересекает
прямую
, пересекает
прямую 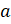 . Тогда про прямые
. Тогда про прямые
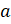 и
и 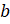 мы можем сказать,
что они параллельны. Записывают это так:
мы можем сказать,
что они параллельны. Записывают это так: 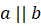 . И говорят: «Прямые
. И говорят: «Прямые
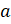 и
и 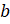 параллельны» или «прямая
параллельны» или «прямая
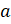 параллельна
прямой
параллельна
прямой 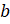 ».
».
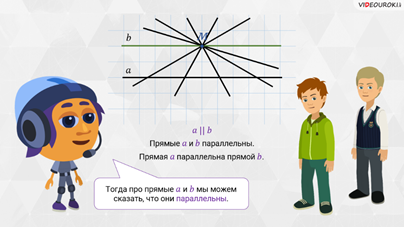
Запомните! Две прямые на плоскости, которые не пересекаются, называют параллельными.

Паша, Саша, может, вы приведёте примеры геометрических фигур, элементы которых лежат на параллельных прямых?
– Думаю, что стороны прямоугольника лежат на параллельных прямых, – предположил Паша.
–
Да. Но только противолежащие стороны прямоугольника лежат на параллельных
прямых. Его соседние стороны перпендикулярны, – сказал Мудряш. – У прямоугольного
параллелепипеда 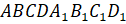 на
параллельных прямых лежат, например, рёбра
на
параллельных прямых лежат, например, рёбра  и
и 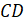 ;
; 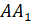 и
и 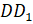 ;
; 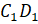 и
и 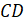 . А как вы думаете,
рёбра
. А как вы думаете,
рёбра 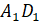 и
и 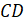 тоже лежат на
параллельных прямых?
тоже лежат на
параллельных прямых?
– Да, ведь они не пересекаются, – сказал Саша.
– Но они не лежат в одной плоскости, – заметил Паша.

– Верно, – сказал Мудряш. – Запомните! Прямые, которые не пересекаются, но не лежат в одной плоскости, называют скрещивающимися.

На
следующем рисунке изображены отрезки 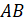 и
и
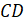 , которые лежат на
параллельных прямых
, которые лежат на
параллельных прямых 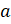 и
и 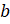 . Такие отрезки
также называют параллельными.
. Такие отрезки
также называют параллельными.

Лучи
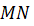 и
и 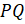 , лежащие на
параллельных прямых
, лежащие на
параллельных прямых  и
и  , также
параллельны.
, также
параллельны.

–
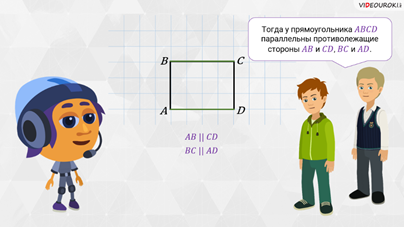
Тогда у прямоугольника 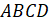 параллельны
противолежащие стороны
параллельны
противолежащие стороны 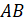 и
и 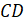 ,
, 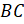 и
и 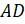 , – догадались мальчишки.
, – догадались мальчишки.
–
Молодцы! – похвалил ребят Мудряш. – В прямоугольном параллелепипеде
параллельными являются, например, рёбра 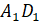 и
и 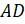 ;
; 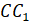 и
и 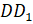 .
.

Ребята,
а теперь посмотрите на рисунок. Здесь прямые 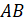 и
и 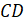 перпендикулярны
прямой
перпендикулярны
прямой 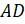 , так как соседние
стороны прямоугольника перпендикулярны. Причём прямая
, так как соседние
стороны прямоугольника перпендикулярны. Причём прямая 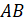 параллельна
прямой
параллельна
прямой 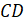 , так как
противолежащие стороны прямоугольника параллельны. Тогда можем сформулировать
следующее свойство.
, так как
противолежащие стороны прямоугольника параллельны. Тогда можем сформулировать
следующее свойство.
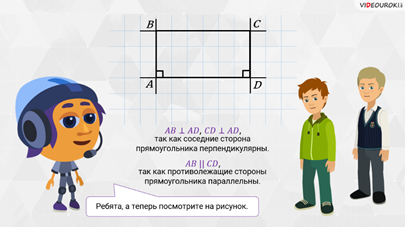
Запомните! Если две прямые, лежащие в одной плоскости, перпендикулярны третьей прямой, то они параллельны.

Построить параллельные прямые мы можем с помощью угольника и линейки.
Давайте
проведём прямую, параллельную прямой 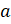 , через точку
, через точку 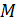 . Для этого мы совместим
сторону прямого угла угольника с прямой
. Для этого мы совместим
сторону прямого угла угольника с прямой 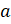 . К другой стороне
прямого угла угольника прикладываем линейку. Теперь двигаем наш угольник вдоль
линейки до тех пор, пока точка
. К другой стороне
прямого угла угольника прикладываем линейку. Теперь двигаем наш угольник вдоль
линейки до тех пор, пока точка 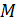 не окажется на
стороне прямого угла угольника. Затем проводим прямую
не окажется на
стороне прямого угла угольника. Затем проводим прямую 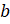 . Прямые
. Прямые 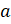 и
и 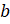 параллельны.
параллельны.

Итак, мы с вами познакомились с параллельными прямыми и умеем их строить.
– Теперь понятно, почему рельсы сравнивают с параллельными прямыми. Ведь они никогда не пересекаются, – разобрались мальчишки.
– Кроме рельсов, представление о параллельных прямых дают нам также провода воздушных линий электропередач, линии дорожной разметки, линии в тетради в линейку, следы, оставленные автомобилем на снегу, который двигался прямолинейно.
– Паша, Саша, а сейчас давайте выполним несколько заданий, – предложил ребятам Мудряш.
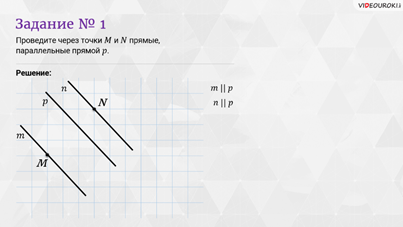
Задание
первое: проведите через точки 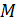 и
и 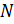 прямые,
параллельные прямой
прямые,
параллельные прямой 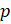 .
.

Решение: строить
прямые, параллельные прямой 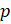 , будем с помощью
угольника и линейки. Сначала проведём прямую, параллельную прямой
, будем с помощью
угольника и линейки. Сначала проведём прямую, параллельную прямой 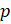 , через точку
, через точку 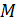 . Для этого совместим
сторону прямого угла угольника с прямой
. Для этого совместим
сторону прямого угла угольника с прямой 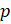 . К другой стороне
прямого угла угольника приложим линейку. Затем будем двигать наш угольник вдоль
линейки, пока точка
. К другой стороне
прямого угла угольника приложим линейку. Затем будем двигать наш угольник вдоль
линейки, пока точка 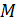 не окажется на
стороне прямого угла угольника. Проведём прямую. Назовём её
не окажется на
стороне прямого угла угольника. Проведём прямую. Назовём её  . Прямые
. Прямые  и
и 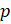 параллельны.
параллельны.
Теперь
проведём прямую, которая будет параллельна прямой 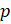 , через точку
, через точку 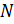 . Совместим
сторону прямого угла угольника с прямой
. Совместим
сторону прямого угла угольника с прямой 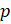 . К другой стороне
прямого угла угольника приложим линейку и будем двигать угольник вдоль линейки
до тех пор, пока точка
. К другой стороне
прямого угла угольника приложим линейку и будем двигать угольник вдоль линейки
до тех пор, пока точка 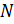 не окажется на
стороне прямого угла угольника. Теперь проведём прямую. Назовём её
не окажется на
стороне прямого угла угольника. Теперь проведём прямую. Назовём её  . Прямые
. Прямые  и
и 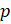 параллельны.
параллельны.
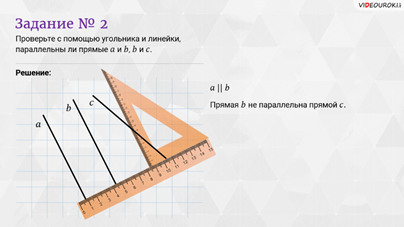
Задание
второе: проверьте с помощью угольника и линейки, параллельны
ли прямые 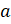 и
и 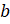 ,
, 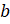 и
и 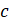 .
.

Решение: проверить,
параллельны ли прямые, можно с помощью угольника и линейки. Возьмём угольник и
совместим сторону его прямого угла с прямой 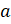 . К другой стороне
его прямого угла прикладываем линейку. Теперь двигаем угольник вдоль линейки до
прямой
. К другой стороне
его прямого угла прикладываем линейку. Теперь двигаем угольник вдоль линейки до
прямой 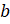 . Видим, что
сторона угольника совместилась с прямой
. Видим, что
сторона угольника совместилась с прямой 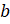 . Значит, прямая
. Значит, прямая 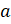 параллельна
прямой
параллельна
прямой 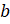 .
.
Продолжим
двигать наш угольник вдоль линейки до прямой 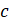 . Видим, что
сторона угольника не совместилась с прямой
. Видим, что
сторона угольника не совместилась с прямой 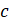 . А значит, прямая
. А значит, прямая
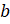 не параллельна
прямой
не параллельна
прямой 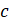 .
.
Следующее
задание: проведите через каждую вершину треугольника 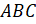 прямую,
параллельную противоположной стороне.
прямую,
параллельную противоположной стороне.

Решение:
проведём
через вершину 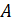 прямую,
параллельную противоположной стороне
прямую,
параллельную противоположной стороне 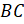 . Возьмём угольник
и совместим сторону его прямого угла с прямой
. Возьмём угольник
и совместим сторону его прямого угла с прямой 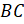 . К другой стороне
его прямого угла приложим линейку и будем двигать угольник вдоль линейки до тех
пор, пока точка
. К другой стороне
его прямого угла приложим линейку и будем двигать угольник вдоль линейки до тех
пор, пока точка 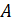 не окажется на
стороне прямого угла угольника. Проведём прямую
не окажется на
стороне прямого угла угольника. Проведём прямую 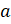 , параллельную
стороне
, параллельную
стороне 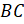 .
.
Теперь
проведём через вершину 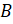 прямую,
параллельную противоположной стороне
прямую,
параллельную противоположной стороне 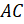 . Возьмём угольник
и совместим сторону его прямого угла с прямой
. Возьмём угольник
и совместим сторону его прямого угла с прямой 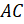 . К другой стороне
его прямого угла приложим линейку и будем двигать угольник вдоль линейки до тех
пор, пока точка
. К другой стороне
его прямого угла приложим линейку и будем двигать угольник вдоль линейки до тех
пор, пока точка 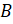 не окажется на
стороне прямого угла угольника. Проведём прямую
не окажется на
стороне прямого угла угольника. Проведём прямую 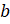 , параллельную
стороне
, параллельную
стороне 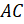 .
.
И
проведём через вершину 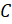 прямую,
параллельную противоположной стороне
прямую,
параллельную противоположной стороне 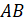 . Возьмём угольник
и совместим сторону его прямого угла с прямой
. Возьмём угольник
и совместим сторону его прямого угла с прямой 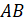 . К другой стороне
его прямого угла приложим линейку и будем двигать угольник вдоль линейки до тех
пор, пока точка
. К другой стороне
его прямого угла приложим линейку и будем двигать угольник вдоль линейки до тех
пор, пока точка 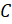 не окажется на
стороне прямого угла угольника. Проведём прямую
не окажется на
стороне прямого угла угольника. Проведём прямую 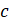 , параллельную стороне
, параллельную стороне
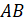 .
.
Таким
образом, мы через каждую вершину треугольника 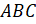 провели прямые,
параллельные противолежащим сторонам.
провели прямые,
параллельные противолежащим сторонам.

И
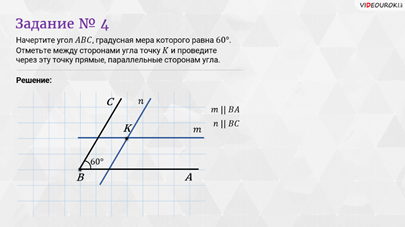
ещё одно задание: начертите угол 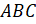 , градусная мера
которого равна
, градусная мера
которого равна 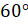 . Отметьте между
сторонами угла точку
. Отметьте между
сторонами угла точку  и проведите через
эту точку прямые, параллельные сторонам угла.
и проведите через
эту точку прямые, параллельные сторонам угла.
Решение: в
первую очередь мы с вами построим угол, равный 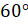 . Для этого
отметим произвольную точку
. Для этого
отметим произвольную точку 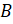 . Затем начертим
луч
. Затем начертим
луч 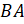 с началом в этой
точке
с началом в этой
точке 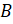 . Теперь приложим
к этому лучу транспортир так, чтобы его центр совпал с точкой
. Теперь приложим
к этому лучу транспортир так, чтобы его центр совпал с точкой 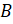 , а сам луч прошёл
через начало отсчёта на шкале. Найдём на шкале транспортира штрих, который
соответствует шестидесяти градусам, и проведём через него луч
, а сам луч прошёл
через начало отсчёта на шкале. Найдём на шкале транспортира штрих, который
соответствует шестидесяти градусам, и проведём через него луч 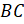 . Таким образом,
мы построили угол
. Таким образом,
мы построили угол 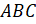 , который равен
, который равен 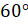 .
.
Отметим
точку  между
сторонами построенного угла. Возьмём угольник и совместим сторону его прямого
угла со стороной
между
сторонами построенного угла. Возьмём угольник и совместим сторону его прямого
угла со стороной 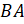 . К другой стороне
его прямого угла приложим линейку и будем двигать угольник вдоль линейки до тех
пор, пока точка
. К другой стороне
его прямого угла приложим линейку и будем двигать угольник вдоль линейки до тех
пор, пока точка  не окажется на
стороне прямого угла угольника. Проведём прямую
не окажется на
стороне прямого угла угольника. Проведём прямую  , параллельную
стороне
, параллельную
стороне 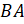 угла
угла 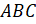 .
.
Затем
сторону прямого угла угольника совместим со стороной 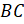 . К другой стороне
прямого угла угольника приложим линейку и будем двигать его вдоль линейки до
тех пор, пока точка
. К другой стороне
прямого угла угольника приложим линейку и будем двигать его вдоль линейки до
тех пор, пока точка  не окажется на
стороне прямого угла угольника. Проведём прямую
не окажется на
стороне прямого угла угольника. Проведём прямую  , параллельную
стороне
, параллельную
стороне 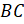 угла
угла 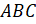 .
.
Итак,
мы провели через точку  прямые
прямые  и
и  , параллельные
соответственно сторонам
, параллельные
соответственно сторонам 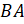 и
и 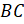 угла
угла 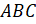 .
.

 Получите свидетельство
Получите свидетельство Вход
Вход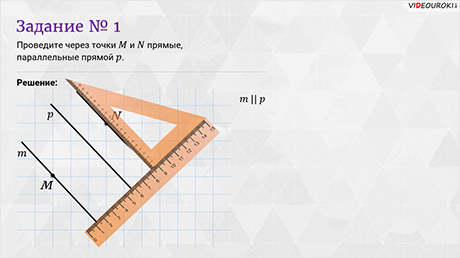



 0
0 3649
3649


