На протяжении школьного курса физики, вы уже много раз слышали о том, что температура является мерой средней кинетической энергии молекул. Но, как сказал Лев Ландау, «верховным судьёй всякой физической теории является опыт». Поэтому, на сегодняшнем уроке мы рассмотрим опыты, позволяющие нам дать определение температуре. Возьмем сосуд с перегородкой и поместим в половинки сосуда два различных газа разной температуры. Если перегородка сосуда проводит тепло, то через некоторое время оба газа будут иметь одинаковую температуру.
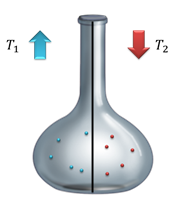
Основываясь на нашем начальном предположении о том, что температура является мерой средней кинетической энергии молекул, мы попытаемся доказать, что средняя кинетическая энергия молекул обладает таким же свойством, как и температура.
Как и было сказано в предыдущих уроках, измерить кинетическую энергию отдельной молекулы крайне сложно. Однако, мы можем выразить среднюю кинетическую энергию молекул газа через макроскопические параметры. Воспользуемся основным уравнением молекулярно-кинетической теории:
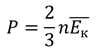
Заметим, что концентрация молекул равна отношению числа молекул газа к его объёму:
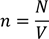
Тогда
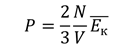
Итак, мы выразили среднюю кинетическую энергию молекул через три величины, которые легко измеряются. Объём можно задать, поместив газ в герметичный баллон, а давление измерим с помощью манометра. Чтобы найти количество молекул, как вы знаете, нужно количество вещества умножить на число Авогадро:
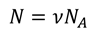
Вспомним теперь, что количество вещества равно отношению массы к молярной массе:
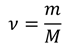
Молярную массу, как вы знаете, можно подсчитать, используя таблицу Менделеева.
Следовательно,
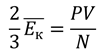
Для проведения опыта мы можем использовать баллоны с водородом и кислородом, давление, объёмы и количество молекул которых, различны.

Чтобы уравнять температуру газов их необходимо привести в тепловое равновесие с одним и тем же телом (как правило, используется тающий лед). Через некоторое время установится тепловое равновесие, то есть температуры кислорода и водорода будут равны 0 оС. Наша цель проверить — уравнялись ли при этом средние кинетические энергии молекул газов, и если это так, то наше начальное предположение верно. Опыты и сопутствующие расчеты говорят о том, что отношение произведения давления и объёма к количеству молекул газа остается постоянным при постоянной температуре, независимо от природы самого газа:
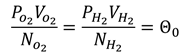
Это говорит нам о том, что средняя кинетическая энергия молекул — это и есть температура.
Необходимо отметить, что данное соотношение все же начинает зависеть от рода газа при очень большом давлении, таком как несколько сотен атмосфер. Однако, мы с уверенностью можем сказать, что до тех пор, пока газ может считаться идеальным, данное соотношение строго определено.
Поскольку температура фактически является мерой энергии, её иногда измеряют в энергетических единицах. Но, дело в том, что в повседневной жизни подобные единицы измерения неудобны. Например, если в баллоне объёмом 10 л находится 1 моль водорода при нормальном давлении, то средняя кинетическая энергия его молекул будет равна 1,68 х 10−21 Дж. В связи с этим возникает вопрос: как перевести температуру из энергетических единиц измерения в градусы, используемые в повседневной жизни? Ведь, люди могут выбирать какую угодно температурную шкалу, но этот выбор не может повлиять на кинетическую энергию молекул. Поэтому, вводится понятие абсолютной температуры. Будем считать эту температуру прямо пропорциональной температуре, выраженной в энергетических единицах:
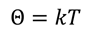
В этой формуле мы обозначили коэффициент пропорциональности буквой k.
Учитывая тот факт, что такие величины, как объём, давление и число молекул, не могут быть отрицательными, делаем вывод, что абсолютная температура тоже не может быть отрицательной.
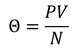
Как видно из формулы, абсолютный ноль температуры — это такая температура, при которой давление газа равно нулю, при постоянном объёме. Такое возможно только в случае, если молекулы газа попросту остановились (это следует из основного уравнения молекулярно-кинетической теории).
Абсолютную шкалу температур предложил лорд Кельвин, в честь которого и названа единица измерения температуры по абсолютной шкале. 1 К равен 1 оС, поэтому перевести градусы Цельсия в кельвины довольно просто: нужно к температуре в градусах Цельсия прибавить 273 градуса:
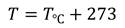
Таким образом, абсолютный ноль температуры по шкале Цельсия равен −273 градуса. Необходимо отметить, что абсолютный ноль недостижим.
Вернемся теперь к уравнению, которое мы использовали в начале урока:
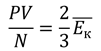
Также, мы выяснили, что отношение произведения давления и объёма к числу молекул должно быть пропорционально температуре:
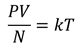
Мы получили два уравнения, левые части которых равны. Значит, должны быть равны и правые части:
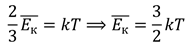
Итак, мы вплотную подошли к связи между средней кинетической энергией и температурой. Остается только разобраться с коэффициентом пропорциональности.
Этот коэффициент получил название постоянной Больцмана, в честь Людвига Больцмана.
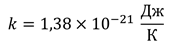
Больцман был первым, кто нашел соотношение между кинетической энергией и температурой. Постоянная Больцмана определяет связь между температурой в энергетических единицах измерения и температурой в кельвинах. Итак, средняя кинетическая энергия молекул равна
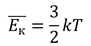
Сегодня мы можем повторить эксперимент, с помощью которого можно вычислить постоянную Больцмана. Возьмем газ, который можно считать идеальным, и измерим среднюю кинетическую энергию его молекул тем же способом, который мы использовали в начале урока — то есть, выразив её через макроскопические параметры:
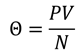
Проведем измерения для двух случаев: в одном случае поместим сосуд в тающий лед, а во втором случае — в кипящую воду.

Тогда, разность между температурами в энергетических единицах измерения должна быть равна произведению разности температуры в кельвинах и постоянной Больцмана:
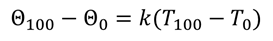
Отсюда выразим постоянную Больцмана:
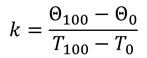
Расчеты показывают, что эта величина остается постоянной для любого газа, который можно считать идеальным:
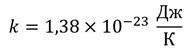
Несмотря на то, что соотношение между температурой и кинетической энергией установлено для газов, оно также выполняется для жидкостей и для твердых тел:
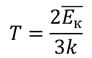
Данное соотношение не выполняется только в том случае, если движение частиц не подчиняется законам механики Ньютона. Это происходит при экстремальных условиях, например при колоссальном давлении, огромной температуре или сильнейших электромагнитных полях.
Пример решения задачи.
Задача. При температуре 200 К средняя скорость молекул одного моля неизвестного газа равна 500 м/с. Считая этот газ идеальным, определите его молярную массу.
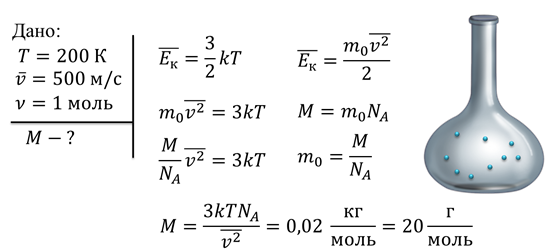

 Получите свидетельство
Получите свидетельство Вход
Вход




 0
0 15040
15040

