На этом уроке мы поговорим о геометрическом теле, которое называют многогранником. А также узнаем, какими элементами обладают многогранники.
Как мы уже знаем, геометрия делится на два раздела – на планиметрию и стереометрию. Планиметрия изучает плоские геометрические фигуры и их свойства, т.е. фигуры, целиком расположенные в некоторой плоскости. Стереометрия изучает свойства фигур в пространстве. Пространственные геометрические фигуры, в отличие от плоских фигур, обладают вместимостью, т.е. они имеют объем. Такие фигуры называют еще объемными.
Все объемные фигуры можно распределить на две большие группы – круглые тела (это цилиндр, конус, сфера и шар), их называют телами вращения, и тела, которые содержат углы, вершины, грани и ребра (это призмы и пирамиды), такие тела называют многогранниками. Представления о геометрических телах дают нам окружающие нас предметы.
Многогранники представляют собой простейшие тела в пространстве, подобно тому, как многоугольники простейшие фигуры на плоскости. С многогранными формами мы ежедневно встречаемся в жизни – это кубики, с которыми играют дети, многогранный карандаш, книги, многоэтажные дома, природные кристаллы, древние египетские пирамиды и т.д.

Ранее, в планиметрии при изучении многоугольников, мы говорили, что многоугольник – это замкнутая ломаная без самопересечений. Или иными словами, многоугольником называется часть плоскости, состоящая из простой замкнутой ломаной и ограниченной ею внутренней области.

При изучении многогранников мы же будем пользоваться вторым толкованием многоугольника.
Итак, уже само слово «многогранник» указывает на то, что это тело имеет много граней. Многогранник представляет собой геометрическое тело, ограниченное конечным числом плоских многоугольников, любые два смежные из которых не лежат в одной плоскости.
Вы хорошо знакомы с одним из самых простых многогранников – прямоугольным параллелепипедом. Представление о прямоугольном параллелепипеде дают, например, спичечный коробок, холодильник, шкаф и другие тела.
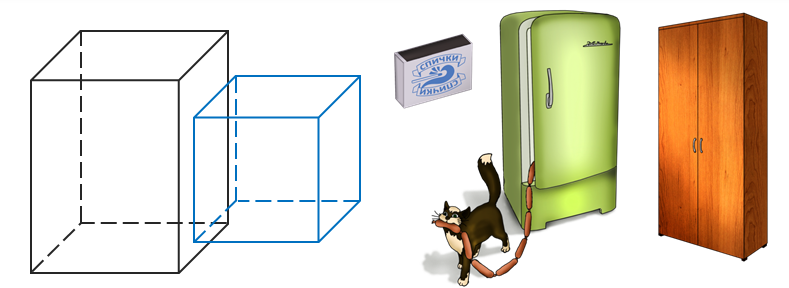
Школьный кабинет также имеет форму прямоугольного параллелепипеда. Поверхность прямоугольного параллелепипеда состоит из 6 прямоугольников. Частным случаем прямоугольного параллелепипеда является куб. Напомню, что поверхность куба состоит из шести равных квадратов.
Можно сказать, что многогранник – это поверхность, составленная из многоугольников и ограничивающая некоторое геометрическое тело. Это тело также называется многогранником.
На рисунке изображены два многогранника.
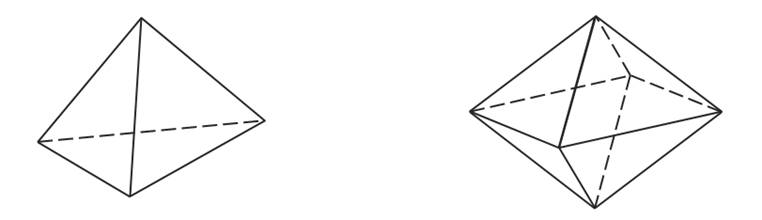
Первый из них называют – тетраэдром, второй – октаэдром. Они составлены соответственно из 4 и 8 треугольников. Что и отражено в их названиях: в переводе с греческого τετρα – «тетра» – четыре, а οκτώ – «окто» – восемь.
Обратим внимание, из чего состоит поверхность многогранника. Давайте рассмотрим, например, прямоугольный параллелепипед ABCDA1B1C1D1.
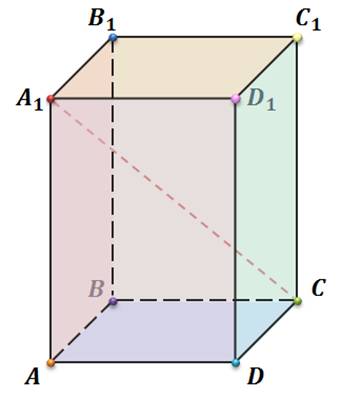
Как уже говорилось ранее, поверхность прямоугольного
параллелепипеда состоит из 6 прямоугольников. Т.е. его поверхность составлена
из 6 многоугольников. Назовем их: 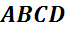 ,
, 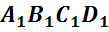 ,
, 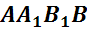 ,
,
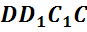 ,
, 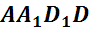 ,
, 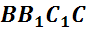 . Многоугольники, из которых
составлен многогранник, называют его гранями. Заметим, что никакие две
соседние грани многогранника не лежат в одной плоскости.
. Многоугольники, из которых
составлен многогранник, называют его гранями. Заметим, что никакие две
соседние грани многогранника не лежат в одной плоскости.
Стороны граней 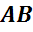 ,
,
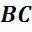 ,
, 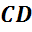 ,
,
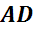 ,
, 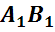 ,
,
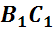 ,
, 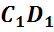 ,
,
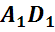 ,
, 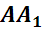 ,
, 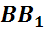 ,
, 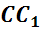 ,
, 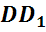
называются ребрами многогранника.
Концы рёбер 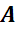 ,
, 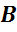 ,
, 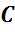 ,
,
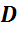 ,
, 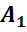 ,
,
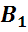 ,
, 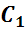 ,
,
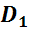 – вершины
многогранника.
– вершины
многогранника.
Отрезок, соединяющий две вершины, не принадлежащие одной грани, называется диагональю многогранника, например, A1C – называется диагональю многогранника. В данном случае, диагональ прямоугольного параллелепипеда.
Многогранники, также как и многоугольники бывают выпуклыми и невыпуклыми.
Смотрите, если провести плоскость, например, через грань DD1C1C, то весь многогранник будет лежать по одну сторону от этой плоскости. Аналогично, если провести плоскости и через остальные его грани, многогранник всегда будет расположен по одну сторону от этих плоскостей. Такой многогранник называется выпуклым.
Определение. Многогранник называется выпуклым, если он лежит по одну сторону от плоскости каждой своей грани.
Если это условие не выполняется, т.е. многогранник лежит по разные стороны хотя бы от одной плоскости, проходящей через грань, то многогранник называется невыпуклым.
На рисунке изображен пример невыпуклого многогранника. Если провести, например, плоскость через указанную грань, то видно, что одна часть многогранника расположена по одну сторону, а вторая его часть по другую сторону этой плоскости.
Задание. Сколько граней, рёбер и вершин имеет каждый из изображенных многогранников?
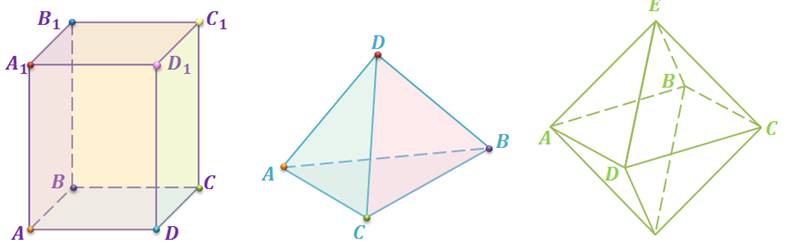
Итак, как мы уже говорили, поверхность прямоугольного параллелепипеда составлена из шести прямоугольников. Т.е. она состоит из 6 граней. Теперь посчитаем, сколько же у него ребер. Напомню, что стороны граней называются ребрами. Назовем их. Это АB, BC, CD, AD, A1B1, B1C1, C1D1, A1D1, AA1, DD1, BB1 и CC1. Итого, получили, что прямоугольный параллелепипед имеет 12 ребер. Концы этих ребер называются вершинами. Перечислим их. Это А, B, C, D, A1, B1, C1, D1. Т.е. у прямоугольного параллелепипеда – 8 вершин.
Следующее геометрическое тело тетраэдр. Его поверхность состоит из четырех треугольников. Т.е. имеет четыре грани. Его ребрами будут стороны АB, BC, АC, AD, BD, и CD. Т.е. тетраэдр имеет 6 ребер. Вершины тетраэдра А, B, C и D. Их 4.
И теперь рассмотрим октаэдр. Его поверхность состоит из 8 треугольников. Т.е. октаэдр имеет 8 граней. Также он имеет 12 ребер и 6 вершин.
Подведем итоги урока. На этом уроке мы узнали, какое геометрическое тело называют многогранником. Рассмотрели, какими элементами обладают многогранники. А именно, это грани, ребра и вершины. Узнали, что прямоугольный параллелепипед имеет 6 граней, 12 ребер и 8 вершин. Познакомились с интересными многогранниками, которые называются тетраэдр и октаэдр. Узнали, что тетраэдр имеет 4 грани, 6 ребер и 4 вершины, а октаэдр – 8 граней, 12 ребер и 6 вершин.

 Получите свидетельство
Получите свидетельство Вход
Вход



 0
0 4465
4465

