Элементы комбинаторики

Вопросы занятия:

·  вспомнить, что изучает комбинаторика;

·  повторить основные виды комбинаций элементов: перестановки, размещения и сочетания;

·  вспомнить, как выводят формулы для их вычисления.

Материал урока

В науке и на практике очень часто встречаются задачи, решая которые приходится составлять различные комбинации из конечного числа элементов, а затем подсчитывать число этих комбинаций.

Такие задачи получили своё название. Их называют комбинаторными задачами.

А раздел математики, в котором рассматриваются подобные задачи, называют комбинаторикой.

Само слово «комбинаторика» происходит от латинского слова combinare, которое означает «соединять, сочетать».

Определение.

Комбинаторика – это раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчинённых тем или иным условиям, можно составить из заданных объектов.

Комбинаторика тесно связана со многими другими областями математики – алгеброй, геометрией, теорией вероятностей. И имеет широкий спектр применения, например, в информатике и статистической физике.

Давайте решим несколько комбинаторных задач.

Задача. Лера, Карина, Глеб и Максим решили сыграть друг с другом по одной партии в бадминтон. Сколько партий было сыграно?

Для краткости имена будем обозначать первой буквой.

Сначала давайте составим все пары, в которых принимала участие Лера. Получим три такие пары.

Теперь составим пары, в которых участвовала Карина, но не принимала участия Лера. Так как пара Лера – Карина у нас уже записана. Таким образом, получим две новые пары.

Затем запишем пары, в которые входит Глеб, но не входят Лера и Карина. Получим только одну пару.

Других вариантов составления пар нет, так как все пары, куда входит Максим, уже составлены.

Итак, мы получили 6 различных пар.

Можем сделать вывод, что было сыграно 6 партий в бадминтон.

Способ рассуждений, которым мы воспользовались при решении задачи, называют перебором возможных вариантов.

Задача.

Определить, сколько различных трёхзначных чисел можно составить, используя цифры 2, 6, 8 и 9. При этом цифры в числе не должны повторяться.

Первой цифрой числа может быть любая из данных цифр.

Поставим на первое место, например, цифру 2. Тогда на втором месте могут стоять цифры 6, 8 или 9. Если на втором месте стоит цифра 6, то на третьем соответственно могут быть цифры 8 или 9. Так мы получим 2 числа: 268 и 269. Если на втором месте стоит цифра 8, то на третьем может быть 6 или 9. Также получим два числа. И если на втором месте стоит 9, то третьей цифрой числа могут быть 6 или 8. Аналогично можно расписать возможные варианты, если первой цифрой числа являются 6, 8 или 9.

Схему, которую мы построили при решении задачи, называют деревом возможных вариантов. И по ней становится понятно, что, используя 4 цифры, можно составить 24 различных трёхзначных числа.

Можно было по-другому решить задачу. Рассуждая так: первую цифру мы выбираем четырьмя способами, вторую тремя, так как после выбора первой осталось три цифры. А третью — двумя. Получаем, что общее количество искомых трёхзначных чисел равно:

При решении данной задачи мы воспользовались комбинаторным правилом умножения.

Этот метод решения комбинаторных задач применяется, когда не требуется перечислять все возможные варианты, а нужно ответить на вопрос — сколько их существует.

Сформулируем его в общем виде.

Пусть имеется  элементов и требуется выбрать из них один за другим  элементов. Если первый элемент можно выбрать  способами, после чего второй элемент можно выбрать  способами из оставшихся, затем третий элемент можно выбрать  способами из оставшихся и так далее, то число способов, которыми могут быть выбраны все  элементов, равно произведению:

В комбинаторике различают три вида различных соединений (комбинаций) элементов фиксированного(конечного) множества. Это перестановки, размещения и сочетания.

И сейчас давайте поговорим о каждом из этих видов поподробнее.

Начнём с перестановок. Кстати, перестановки – это простейшие комбинации, которые можно составить из элементов конечного множества.

Вот, например. Пусть есть 3 книги. Обозначим их буквами a, b и c. Понятно, что эти книги мы можем расставить на полке совершенно разными способами.

Если первой поставить книгу а, то возможны такие расположения книг на полке: a, b, c и a, c, b.

Если первой поставить книгу b, то возможными будут такие расположения книг: b, a, c и b, c, a.

Ну, а если же первой поставить книгу c, то можно получить следующие расположения книг на полке: c, a, b и c, b, a.

Заметим, мы получили 6 возможных расположений книг на полке.

Каждое из этих возможных расположений книг называют перестановкой из трёх элементов.

Определение.

Перестановкой из  элементов называется каждое расположение этих элементов в определённом порядке.

Напомним, что число перестановок из  элементов обозначают так:

и говорят « из ».

Вернувшись к рассмотренному примеру, можно сказать, что число перестановок из трёх элементов .

Это же значение мы могли бы получить, пользуясь комбинаторным правилом умножения:

Т.е. для выбора первого элемента существует 3 варианта. Для каждого из них есть 2 варианта выбора второго элемента. И третий элемент мы выбираем единственным способом.

Значит, число перестановок из трёх элементов действительно равно 6.

А теперь давайте вспомним, как выводится формула числа перестановок из  элементов.

Пусть у нас есть  элементов. Тогда на первое место можно поставить один из них, то есть  вариантов. На второе место можно поставить любой из оставшихся «» элементов. На третье место можно поставить любой из оставшихся «» элементов. И так далее … . В результате получим следующую запись:

Расположив множители в порядке возрастания, получаем формулу числа перестановок из  элементов:

Кстати, для записи произведения первых  натуральных чисел есть специальное обозначение  .А читают его « факториал».

Например, .

По определению считают, что .

Таким образом, число всевозможных перестановок из  элементов вычисляется по формуле: .

Например, найдём число перестановок из 5 элементов.

Задача.

Имеется 9 карандашей, 4 из которых — простые. Сколькими способами можно разложить их в коробке так, чтобы все простые карандаши лежали рядом?

Сначала все простые карандаши давайте условимся рассматривать как один карандаш. Тогда нам нужно разложить в коробке не 9, а 6 карандашей.

Найдём сколькими способами это можно сделать. Т.е. имеем, число перестановок из 6 элементов равно .

В каждом из полученных способов 4 простых карандаша тоже можно разложить по-разному. А точнее .

Для нахождения общего числа способов нужно . В ответ запишем 17280 способов.

Теперь перейдём к следующему виду комбинаций – размещения.

И начнём с примера. Пусть есть 4 шара и 3 пустые ячейки. В каждую ячейку можно поместить только по одному шару. Для удобства обозначим шары буквами: А, B, C и D.

Если поместим шар А в первую ячейку, шар B — во вторую ячейку, а шар C — в третью, то мы получим одну из возможных упорядоченных троек шаров.

Выбирая по-разному шары для каждой из ячеек, получим, например, такие тройки:

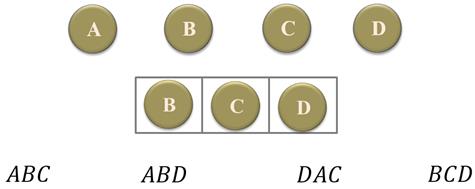
Каждую такую упорядоченную тройку, составленную из 4 элементов, называют размещением из 4 элементов по 3.

Определение.

Размещением из  элементов по , где , называется любое множество, состоящее из  элементов, взятых в определённом порядке из данных  элементов.

Два размещения из  элементов по  считаются различными, если они различаются самими элементами или порядком их следования.

Число размещений из  элементов по  обозначают так:

И читают « из  по ».

Вернёмся к примеру. Можем обозначить число размещений из четырёх элементов по три таким образом: .

Вычислим количество таких размещений для данного случая, пользуясь правилом комбинаторного умножения. Первый элемент мы выбирали одним из 4 способов, так как им может быть любой из 4 шаров. Второй элемент мы можем выбрать 3 способами и третий — 2. Так получаем, что число размещений из 4 элементов по 3 равно

С помощью таких же рассуждений можно вывести формулу для вычисления числа размещений из  элементов по .

Для выбора первого элемента можно взять любой из  элементов, то есть существует  способов. Для выбора второго элемента можем взять любой из «» оставшихся элементов, то есть «» способов. Третий элемент можно выбрать «» способами. И так далее … . Так  -ый элемент можно выбрать «» способами.

Умножим и разделим правую часть этого равенства на «». Заменим  произведением и расположим множители в порядке возрастания. Заметим, что в числителе записано произведение всех натуральных чисел от 1 до  включительно. А ведь это произведение равно .

Мы получили формулу для вычисления числа размещений из  элементов по  при .

Стоит обратить внимание на то, что размещения из  элементов по  отличаются только порядком следования элементов, так как каждый из них должен участвовать в размещении. Тогда получаем, что такое размещение является перестановкой.

Рассмотрим пример: вычислить число размещений из 5 элементов по 3.

Воспользовавшись формулой размещений, получим,

Задача.

Девять карточек пронумерованы цифрами от 1 до 9. Из этих карточек 4 наугад выкладывают в ряд. Сколько при этом различных четырёхзначных чисел можно получить?

Суть задачи состоит в том, что из 9 данных цифр нужно составить всевозможные четырёхзначные числа, не повторяя цифры в числе. Следовательно, решение задачи сводится к отысканию числа размещений из 9 элементов по 4.

Запишем формулу для нахождения числа размещений. Представим числитель и знаменатель в виде произведения. Сократим дробь. Остаётся вычислить произведение. В результате получим,

Значит, можно получить 3024 различных четырёхзначных числа.

Ну а теперь давайте поговорим о последнем виде комбинаций элементов, о сочетаниях.

Начнём с примера. Пусть имеются 5 цветков различного цвета. Для удобств обозначим их буквами: А, B, C, D и Е. Будем составлять букеты из 3 цветков.

Если в букет входит цветок А, то можем составить такие букеты:

АBC, АBD, АBЕ, АCD, АCЕ, и АDЕ.

Если в букет входит цветок B, но не входит А, то составим букеты:

BCD, BCЕ, и BDЕ.

Если же в букет входит цветок C и не входят А и B, то получим только один букет: CDЕ.

Так мы с вами указали все возможные способы составления букетов, в которых по-разному сочетаются 3 цветка из данных 5.

Таким образом, мы составили все возможные сочетания из 5 элементов по 3.

Определение.

Сочетанием из  элементов по  называется любое множество, составленное из  элементов, выбранных из данных  элементов.

Число сочетаний из  элементов по  обозначают так:

И читают « из  по ».

В отличие от размещений в сочетаниях не имеет значения, в каком порядке расположены элементы. Сочетания считаются различными, если они отличаются хотя бы одним элементом.

Так, например, такие два букета

являются размещениями. Так как в их состав входят одни и те же элементы, только с разным расположением.

А два таких букета

являются сочетаниями, ведь они отличаются составом элементов.

В рассмотренном примере мы составили все сочетания из 5 элементов по 3. И выяснили, что их число равно 10.

Вспомним, как выводится формула числа сочетаний из  элементов по .

Допустим, что имеется множество из  элементов, и из них составлены все возможные сочетания по  элементов. Число таких сочетаний равно . В каждом из этих сочетаний можно выполнить  перестановок. В результате мы получим все размещения, которые можно получить из  элементов по . Получим такую запись.

Из неё следует, что число сочетаний из  элементов по  равно частному «числа размещений из  элементов по » и «числа перестановок из  элементов».

Пользуясь уже известными формулами числа перестановок и размещений, получим такое равенство.

Так мы с вами получили формулу нахождения числа сочетаний из  элементов по . При этом .

Рассмотрим пример: найти число сочетаний из 7 элементов по 4.

По формуле сочетаний имеем:

Задача.

Турист запланировал взять с собой в поездку 8 футболок, при этом всего их у него насчитывается 12. Сколькими способами он может сделать выбор?

Применим формулу сочетаний из  элементов по . У вас мог возникнуть вопрос, почему мы не ищем число размещений? Но вспомнив отличие размещений от сочетаний, становится ясно, что туристу не важно, в каком порядке он соберёт футболки. Ему важно, какие именно из них он возьмёт с собой.

Итак, запишем формулу числа сочетаний из 12 элементов по 8. Получаем,

Итоги урока

На этом уроке мы рассмотрели тему «элементы комбинаторики». Вспомнили, что изучает комбинаторика. Повторили, основные виды комбинаций элементов: перестановки, размещения и сочетания. И вспомнили, как выводят формулы для их вычисления.