Измерение углов. Транспортир

На этом уроке мы познакомимся с прибором для измерения углов – транспортиром. Научимся с помощью транспортира измерять и строить углы.

Коснёмся истории, чтобы узнать, как появился транспортир.

Понятие «градуса» и появление первых инструментов для измерения углов связывают с развитием цивилизации в древнем Вавилоне. Хотя само слово градус имеет латинское происхождение (градус – от лат. gradus – “шаг, ступень”). Предполагают, что создание транспортира было связано с созданием первого календаря.

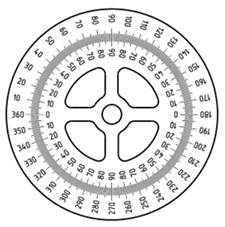
Древние вавилонские математики и астрономы полный оборот (окружность) разделили на столько частей, сколько дней в году. Они думали, что в году 360 дней. Поэтому круг, обозначающий год, они разделили на 360 равных частей. Такое изображение было очень удобным. На нём можно было отмечать каждый прошедший день, и видеть, сколько дней осталось до конца года. Каждой части дали название – градус. Каждый градус разделили на 60 минут, а минуту – на 60 секунд. Градусная мера сохранилась и до наших дней.

Итак, для измерения углов применяют транспортир.

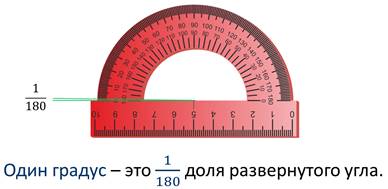
Транспортир состоит из линейки (прямолинейной шкалы) и полуокружности (угломерной шкалы). Центр этой полуокружности отмечен на транспортире или штрихом, или отверстием. Штрихи шкалы транспортира делят полуокружность на 180 долей. В некоторых моделях – на 360 долей – это круглые транспортиры.

Если из центра этой полуокружности провести лучи через каждый штрих, то получится 180 углов. Каждый, из которых равен 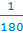 доле развернутого угла.

Определение

Такие углы принято называть градусами. 

Градусы обозначают вот таким знаком °.

Каждое деление шкалы транспортира равно 1°. Кроме делений по 1° на шкале транспортира есть ещё деления по 5° и по 10°.

А теперь давайте разберёмся, как с помощью транспортира измерить угол. Запомните алгоритм измерения углов:

1)  Совместить вершину угла с центром транспортира.

2)  Расположить транспортир так, чтобы одна из сторон угла проходила через начало отсчёта на шкале транспортира; 0 – начало отсчёта.

3) Найдём штрих на шкале, через который пройдёт вторая сторона угла; (заметьте, используем ту шкалу для определения градусной меры угла, где располагается нулевой градус).

4)  Смотрим, через какой штрих проходит вторая сторона и какой градус соответствует этому штриху.

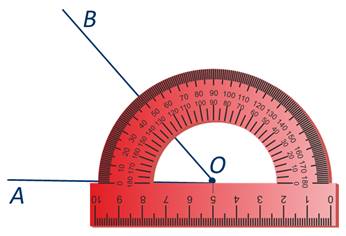
На нашем слайде угол АОВ равен 50°. Пишут так: 

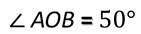
Развёрнутый угол равен 180°. Так как мы с вами выяснили, что прямой угол равен половине развёрнутого угла, то он равен

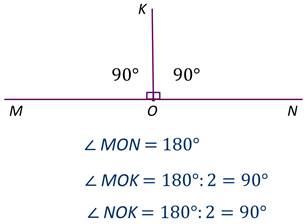
Прямой угол равен 90°.

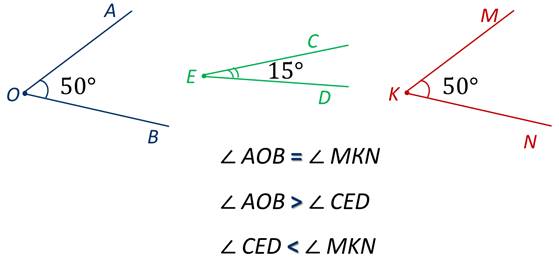
Так как равные углы полностью совмещаются при наложении, то равные углы имеют равные градусные меры. Следовательно, больший угол имеет большую градусную меру, меньший угол имеет меньшую градусную меру.

Транспортир применяют и не только для измерения углов, а также и для их построения.

Запомним алгоритм построения углов.

Алгоритм будем исследовать на конкретном примере: построить угол МКN равный 110°.

1.     Отметим произвольную точку и обозначим её буквой К.

2.     Начертим луч с началом в точке А и на нём отметим произвольную точку М. Получили луч КМ.

3.     Наложим транспортир так, чтобы центр его совпал с точкой К, а луч КМ прошёл через начало отсчёта на шкале.

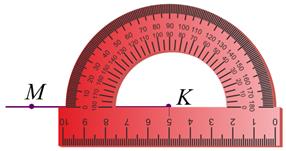
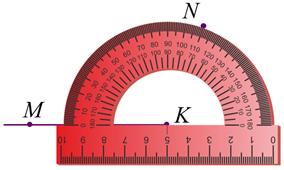
4.     На этой же шкале транспортира найдём штрих, который соответствует 110°. Отметим на чертеже точку N против штриха с отметкой 110°.

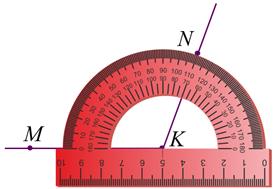
5.     Проведём луч КN. Построенный нами угол МКN и есть искомый.

6.     Не забудем записать МКN = 110°.

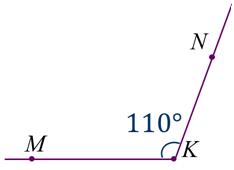
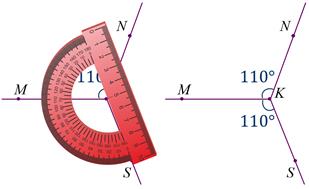
Такой же угол можно построить и по другую сторону от луча КМ.

Повсюду есть углы любые:
Прямые, острые, тупые,
Есть смежные, развёрнутые есть,
Их много, всех не перечесть.

Определение

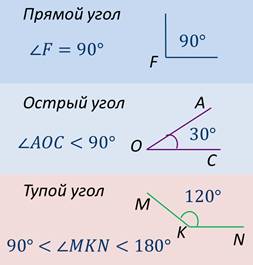
Если угол меньше 90°, то его называют острым углом.

Если угол больше 90°, но меньше 180°, то его называют тупым углом.

На экране изображены угол АОС – острый и угол МКN – тупой. Градусная мера угла АОС равна 30°, т.е. меньше 90°, следовательно, он острый. Градусная мера угла МКN равна 120°, т.е. больше 90°, но меньше 180°, следовательно, он тупой.

Итоги

Итак, сегодня на уроке мы познакомились с прибором для измерения углов – транспортиром. Научились с помощью него измерять и строить углы.