Угол. Прямой и развернутый угол. Чертежный треугольник

На этом уроке мы узнаем, что за фигуру называют углом. Рассмотрим элементы, которыми обладает угол. А также рассмотрим взаимное расположение угла и точек.

Для начала вспомним основные плоские геометрические фигуры, которые мы с вами научились уже строить в курсе математики 5-го класса.

Напомним, что плоские геометрические фигуры – это фигуры, которые располагаются в плоскости.

Например,

А теперь давайте перейдём непосредственно к чертежам. Отметим в плоскости, в любом понравившемся вам месте, некоторую точку О. И проведём от этой точки два луча ОА и ОВ. Обратите внимание, у нас получилась новая геометрическая фигура, угол.

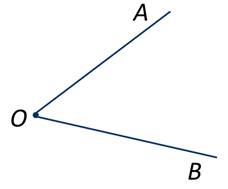
Определение

Угол – это часть плоскости, ограниченная двумя лучами, выходящими из одной точки, или имеющими одно начало.

Угол визуально делят на «внешний» и «внутренний».

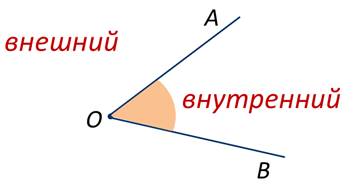
Мы же все чаще будем работать именно с внутренними углами.

Определение

У нас получился угол АОВ. Называют его заглавными латинскими буквами и обозначают угол вот таким знаком «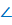», который вам следует не перепутать со знаком «меньше».

Лучи ОА и ОВ – называют сторонами угла, а точку О – его вершиной. При записи угла в середине пишут его вершину.

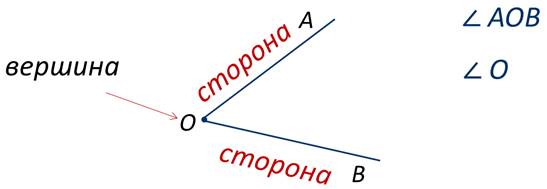
Обратите внимание угол, который мы построили имеет вершину точку О, и в записи угла буква О стоит в середине. Также угол можно записать одной буквой, обозначающей его вершину, т.е. в нашем случае можно записать угол О.

Рассмотрим взаимное расположение угла и точек на плоскости.

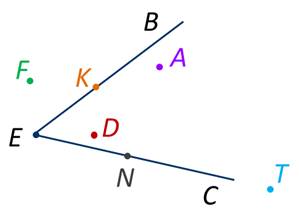
На экране изображён угол ВЕС и 6 точек A, D, F, K, N, T.

Углы, как и любые геометрические фигуры можно сравнивать. А сравнивают их при помощи наложения.

Запомните: два угла называют равными, если их можно наложить один на другой так, что их вершины и стороны совпадут.

Например

На экране изображены три угла АОВ, CED и MKN.

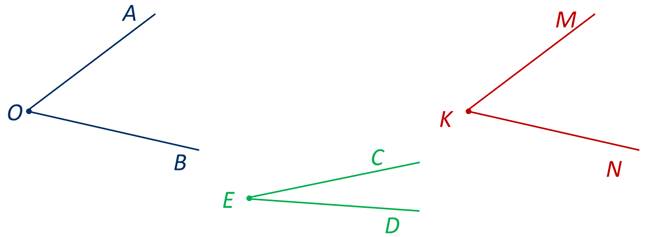
Давайте сравним угол АОВ с углами CED и MKN.

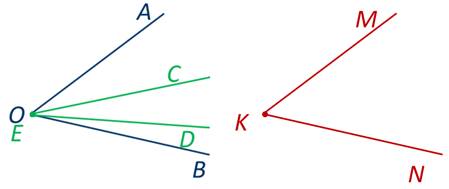
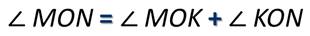
Изобразим следующий рисунок. Начертим угол MON и из его вершины точки О проведём луч ОК.

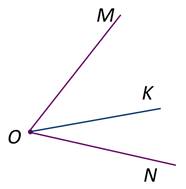
Обратите внимание луч ОК разделяет наш начальный угол MON на два угла МОК и КОN, каждый из этих углов меньше угла MON. Пишут так:

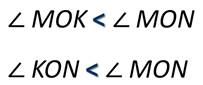
А вместе два этих угла образуют угол MON. Записать это можно так

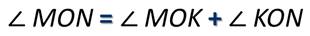
Определение

Два дополнительных друг другу луча образуют развёрнутый угол.

Сторонами такого угла является прямая линия, на которой лежит вершина развёрнутого угла.

Посмотрите внимательно на экран.

Лучи ОА и ОВ являются дополнительными друг другу.

Они образуют развёрнутый угол АОВ.

Точка О – вершина развёрнутого угла лежит на прямой АВ.

Пример развёрнутого угла вы можете встретить каждый день.

Например

Мы помним, что прямые могут пересекаться. При пересечении двух прямых образуются 6 углов, 2 из которых – развёрнутые.

Например

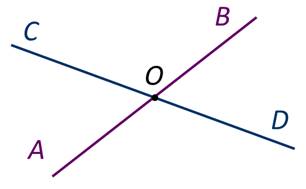
Прямые АВ и СD пересекаются в точке О. Угол АОВ – развёрнутый и угол СОD – развёрнутый.

Начертим развёрнутый угол MON и проведём из его вершины луч ОК, так чтобы этот луч разделил угол MON на 2 равных угла.

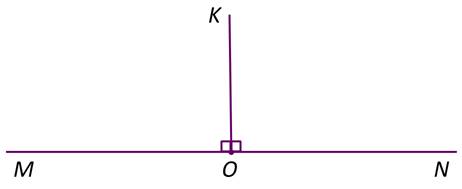
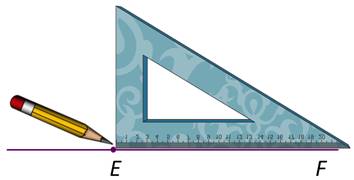
У нас получились углы МОК и NОК. Эти углы равны между собой и равны половине развёрнутого угла. Записывают это так:

Такие углы называют прямыми.

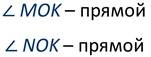
Для построения прямого угла пользуются чертёжным треугольником.

Запомните алгоритм построения прямого угла.

Для того чтобы построить прямой угол, стороной которого является луч EF, надо:

1)    Расположить чертёжный треугольник так, чтобы его вершина совпала с точкой Е, а одна из его сторон пошла по лучу EF.

2)    Провести луч ЕС вдоль второй стороны чертёжного треугольника.

3)    Угол СEF, который образовался после выполнения 1–го и 2–го шага алгоритма и есть прямой.

Итоги

Итак, сегодня на уроке мы узнали, что за фигуру называют углом. Рассмотрели элементы, которыми обладает угол. Изучили взаимное расположение угла и точек в плоскости. Узнали, какие углы называют прямыми и развёрнутыми. А также научились пользоваться чертёжным треугольником.