Проценты

На этом уроке мы познакомимся с новой величиной, которую называют «процент». Узнаем, как вычисляют проценты. А также применим знания при решении задач.

Наверняка, каждый из вас в жизни слышал и не раз слово «процент».

Например

Слово процент произошло от латинского слова «pro centum», что буквально означает «за сотню» или «со ста». Идея выражения частей целого постоянно в одних и тех же долях, вызванная практическими соображениями, родилась ещё в древности у вавилонян. Проценты были особенно распространены в Древнем Риме. Римляне называли процентами – деньги, которые платил должник заимодавцу за каждую сотню.

От римлян проценты перешли к другим народам Европы. Долгое время под процентами понимались исключительно прибыль или убыток на каждые сто рублей. Они применялись только в торговых и денежных сделках.

Затем область их применения расширилась, проценты встречаются в хозяйственных и финансовых расчётах, статистике, науке и технике.

Определение

Процент – это одна сотая часть любой величины или числа. 

Знак % происходит, как полагают, от итальянского слова cento (сто), которое в процентных расчётах часто писалось сокращённо cto. Отсюда путем дальнейшего упрощения в скорописи буква t превратилась в наклонную черту (/), возник современный символ для обозначения процента.

Попробуем разобраться, почему же для процента берут именно сотую часть. Мы помним, что сотую часть метра называют сантиметром, сотую часть гектара – аром или соткой. Удобно выделять сотую часть. Также вы знаете, что удобнее работать с десятичными дробями, нежели с обыкновенными. Поэтому и стало принято называть сотую часть любой величины или числа процентом.

Отсюда следует, что

Проценты очень тесно связаны с дробями, как с обыкновенными, так и с десятичными.

Чтобы перевести десятичную дробь в проценты, нужно дробь умножить на 100 и добавить знак %.

Например

Переведём десятичные дроби в проценты: 0,2; 0,18 и 0,04.

Чтобы перевести обыкновенную дробь в проценты, нужно сначала перевести её в десятичную дробь, а потом умножить на 100 и добавить знак %.

Например

Переведём дроби в проценты: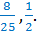  

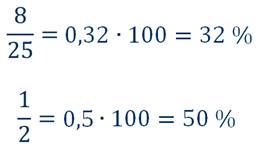
Чтобы проценты перевести в число, нужно убрать знак % и разделить число на 100.

Например

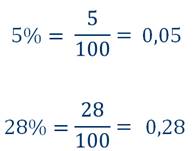
Как переводить дроби в проценты и наоборот, проценты в числа думаю разобрались. Теперь давайте разберёмся, как решать задачи с помощью процентов.

Задача 1

В магазин привезли 650 кг фруктов. Из них 28 % составляли апельсины. Сколько кг апельсинов привезли в магазин?

Решение

Задача 2

До конца урока осталось 9 минут. Известно, что это составляет 20 % от всего урока. Сколько минут длится весь урок?

Решение

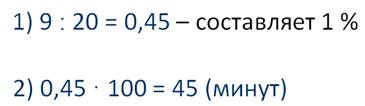
Задача 3

В палисаднике возле школы посадили 50 роз. 15 роз белого цвета. Сколько процентов от всех роз составляют белые розы?

Решение

Как вы поняли, проценты тесно связаны с обыкновенными и десятичными дробями. Поэтому стоит запомнить несколько простых равенств.

Посмотрите внимательно на экран, вы видите таблицу соотношений:

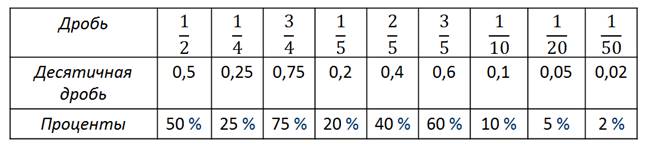
В повседневной жизни нужно знать о числовой связи дробей и процентов.

Так,

Знание наизусть соотношений из таблицы облегчит вам решение многих задач.

Итоги

Итак, сегодня на уроке мы познакомились с новой величиной, которую называют «процент». Узнали, как вычисляют проценты и применили свои знания при решении задач.