Прежде чем приступить к изучению нового материала давайте повторим, что если каждой точке плоскости ставится в соответствие какая-то точка этой же плоскости, причем любая точка плоскости оказывается сопоставленной некоторой точке, тогда говорят, что дано отображение плоскости на себя.
Вспомним, что движение плоскости – это отображение плоскости на себя, сохраняющее расстояния.
Мы уже познакомились и повторили некоторые виды движения: такие как осевая симметрия, центральная симметрия, параллельный перенос.
Сегодня на уроке мы познакомимся с еще одним видом отображения плоскости на себя – поворотом.
Давайте отметим на плоскости произвольную точку О, назовем ее центром поворота, и зададим угол α (назовем его углом поворота).
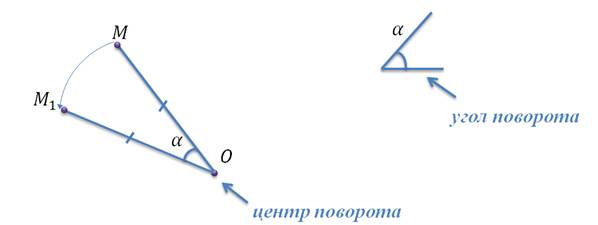
Поворотом плоскости
вокруг точки О на угол α называется отображение плоскости на себя, при
котором каждая точка М отображается в такую точку М1, что 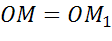 и угол MOM1=α. Заметим, что
точка О остается на месте, то есть другими словами, отображается сама в себя, а
все остальные точки поворачиваются вокруг точки О, причем, если
и угол MOM1=α. Заметим, что
точка О остается на месте, то есть другими словами, отображается сама в себя, а
все остальные точки поворачиваются вокруг точки О, причем, если 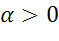 , то против часовой стрелки, если
, то против часовой стрелки, если 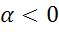 , то по часовой стрелке
, то по часовой стрелке
Иногда в литературе
можно встретить следующее обозначение для поворота вокруг центра О и на угол
α: 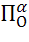 .
.
Теперь давайте попробуем определить, будет ли поворот движением? Для этого достаточно показать, что при повороте сохраняется расстояние между точками.
Пусть точка О – центр поворота, а угол α– угол поворота.
Рассмотрим случай, когда α>0, то есть поворачивать относительно точки О будем против часовой стрелки. Случай, когда α<0, то есть случай, когда поворачивать будем по часовой стрелке рассматривается аналогично, это вы можете сделать самостоятельно.

Пусть при этом повороте точки М и N отображаются в точки M1 и N1 соответственно. Рассмотрим треугольники ОМN и OM1N1.
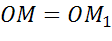

 ,
, 

 , другими словами, при повороте расстояние
между точками сохраняется. Значит, поворот – это еще один вид движения. Его
можно представить себе как поворот всей плоскости вокруг данной точки О на
данный угол α.
, другими словами, при повороте расстояние
между точками сохраняется. Значит, поворот – это еще один вид движения. Его
можно представить себе как поворот всей плоскости вокруг данной точки О на
данный угол α.
Задача. Построить
отрезок  , который получается из отрезка
, который получается из отрезка  поворотом вокруг данного центра
поворотом вокруг данного центра  на:
на:
а)  , б)
, б)  , в)
, в)  .
.
Решение.
Для поворота отрезка, повернем концы этого отрезка. Для того, чтобы повернуть точку А, построим прямую ОА. От точки О с помощью транспортира отметим 150° (мы помним, что если угол меньше 0, то поворачиваем по часовой стрелки, то есть угол будем откладывать в эту сторону). С помощью циркуля измеряем расстояние АО и отложим это расстояние на получившейся прямой.

Поставим точку А1. Аналогично, построим точку B1. Тогда получившийся отрезок A1B1 – искомый. Для того, чтобы выполнить поворот на 100°, надо 100° отложить против часовой стрелки.

Все остальные построения проводятся аналогично тому, как мы делали в первом пункте. При повороте на 180° точка A1 будет лежать на продолжении прямой ОА. Точка B1 будет лежать на продолжении прямой OB.

Задача. Постройте
треугольник, который получается из данного треугольника  поворотом вокруг:
поворотом вокруг:
а) точки  на
на  ,
,
б) вокруг точки  , не лежащей внутри треугольника на
, не лежащей внутри треугольника на  ,
,
в) вокруг точки  , лежащей внутри треугольника на
, лежащей внутри треугольника на  .
.
Решение.
Строить треугольник будем по точкам. Поскольку центром поворота является точка А, то она отображается сама на себя. Отобразим точку B. От точки А отложим против часовой стрелки угол равный 80°. Отложим на этой прямой отрезок равный стороне AB и получим точку B1. Аналогично построим точку C1. Тогда треугольник AB1C1 – искомый.
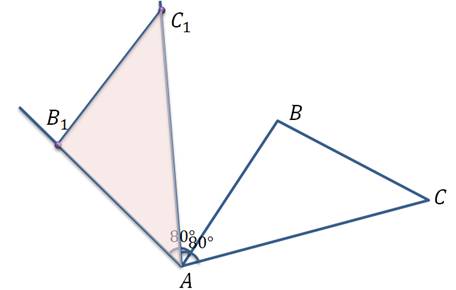
Проведя аналогичные построения, построим треугольники A1B1C1 для остальных двух случаев.


Сегодня мы заканчиваем с вами изучение темы Движение. Давайте еще раз вспомним, что такое движение и с какими видами движения мы успели познакомиться.
Движение плоскости – это отображение плоскости на себя, сохраняющее расстояния.
Мы доказали, что движением являются: осевая симметрия, центральная симметрия, параллельный перенос и поворот.

 Получите свидетельство
Получите свидетельство Вход
Вход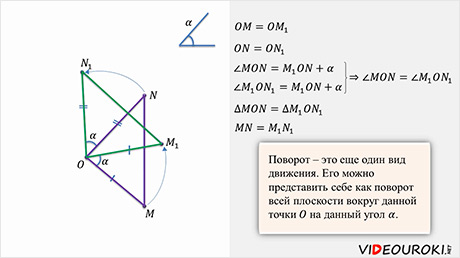



 0
0 17024
17024