Прежде чем приступить к изучению нового материала, давайте вспомним, что если каждой точке плоскости ставится в соответствие какая-то точка этой же плоскости, причем любая точка плоскости оказывается сопоставленной некоторой точке, тогда говорят, что дано отображение плоскости на себя.
Вспомним, что движение плоскости – это отображение плоскости на себя, сохраняющее расстояния.
Напомним, что при движении отрезок отображается на отрезок, треугольник отображается на треугольник, угол отображается на равный ему угол.
Сегодня мы с вами познакомимся с еще одним видом преобразования – параллельным переносом.
Преобразование, при котором каждая точка фигуры перемещается в одном и том же направлении и на одно и то же расстояние называется параллельным переносом.
Для того, чтобы
задать перенос достаточно задать вектор. Другими словами параллельным
переносом на вектор  называется отображение плоскости на себя, при котором каждая точка
называется отображение плоскости на себя, при котором каждая точка  отображается
в такую точку
отображается
в такую точку  ,
что вектор
,
что вектор  равен
вектору
равен
вектору  .
.

Теперь давайте попробуем определить, будет ли параллельный перенос движением.
Пусть при
параллельном переносе на вектор  точки
М и N отображаются в точки М1 и N1.
точки
М и N отображаются в точки М1 и N1.

 ,
, 
 ,
,  параллелограмм
параллелограмм

Случай, когда точки
М и N лежат на прямой параллельной вектору  вы можете рассмотреть
самостоятельно, но и в этом случае расстояние между точками М и N будет равно расстоянию между
точками M1 и N1.
Таким образом, параллельный перенос сохраняет расстояние между точками и
поэтому представляет собой движение. Это движение можно представить себе как
сдвиг всей плоскости в направлении данного вектора
вы можете рассмотреть
самостоятельно, но и в этом случае расстояние между точками М и N будет равно расстоянию между
точками M1 и N1.
Таким образом, параллельный перенос сохраняет расстояние между точками и
поэтому представляет собой движение. Это движение можно представить себе как
сдвиг всей плоскости в направлении данного вектора  на его длину.
на его длину.
Для параллельного переноса как и для движения можно перечислить несколько свойств.
При параллельном переносе отрезок переходит в равный ему отрезок. Угол переходит в равный ему угол. Окружность переходит в равную ей окружность. Любой многоугольник переходит в равный ему многоугольник. Параллельные прямые переходят в параллельные прямые. Перпендикулярные прямые переходят в перпендикулярные прямые.

Решим несколько задач.
Задача. Начертить
отрезок  и вектор
и вектор  . Построить отрезок
. Построить отрезок  , который получится из
отрезка
, который получится из
отрезка  параллельным переносом на
вектор
параллельным переносом на
вектор  .
.
Решение.
Для того, чтобы построить отрезок A1B1, отобразим точку А в точку A1, точку B в точку B1 с помощью параллельного переноса. Тогда соединив точки A1 и B1 мы получим отрезок A1B1.
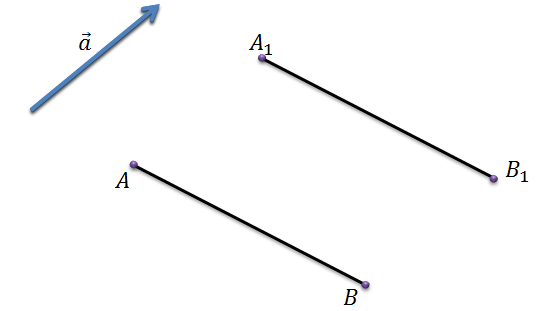
Задача. Начертить
треугольник  и вектор
и вектор  . Построить треугольник
. Построить треугольник  , который получится из
треугольникa
, который получится из
треугольникa  параллельным переносом на
вектор
параллельным переносом на
вектор  .
.
Решение.
Отобразим с помощью параллельного переноса точки А, B, C в точки А1, B1, C1. Соединив полученные точки, мы получим искомый треугольник А1 B1 C1.
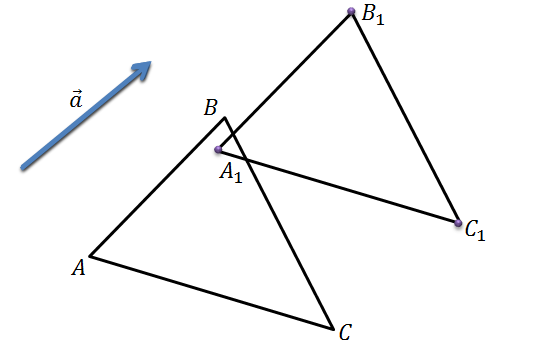
Задача. Начертить
пятиугольник  и вектор
и вектор  . Построить пятиугольник
. Построить пятиугольник  , который получится из
пятиугольника
, который получится из
пятиугольника  параллельным переносом на
вектор
параллельным переносом на
вектор  .
.
Решение.
Решать эту задачу
будем аналогично тому как мы решали предыдущую задачу. Отобразим каждую вершину
пятиугольника с помощью параллельного переноса на вектор  . Соединим получившиеся
точки и получим искомый пятиугольник A1B1C1D1E1.
. Соединим получившиеся
точки и получим искомый пятиугольник A1B1C1D1E1.
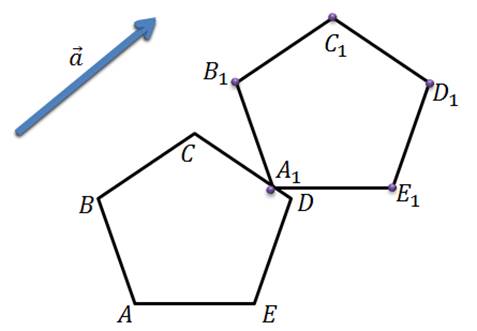
Подведем итоги урока. Сегодня мы
познакомились с еще одним видом движения – параллельным переносом.
Преобразование, при котором каждая точка фигуры перемещается в одном и том же
направлении и на одно и то же расстояние называется параллельным переносом.
Чтобы задать параллельный перенос, достаточно задать некоторый вектор. Другими
словами параллельным переносом на вектор  называется
отображение плоскости на себя, при котором каждая точка М отображается в такую
точку M1, что вектор
называется
отображение плоскости на себя, при котором каждая точка М отображается в такую
точку M1, что вектор  равен
вектору
равен
вектору  .
.

 Получите свидетельство
Получите свидетельство Вход
Вход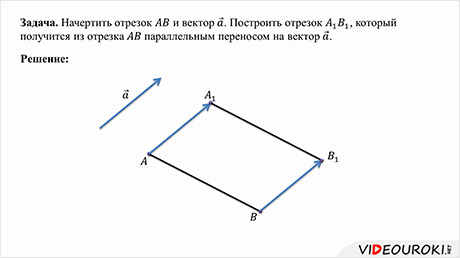



 0
0 10051
10051

