Прежде чем приступить к изучению нового материала давайте вспомним, что если каждой точке плоскости ставится в соответствие какая-то точка этой же плоскости, причем любая точка плоскости оказывается сопоставленной некоторой точке, то говорят, что дано отображение плоскости на себя.
Фигура называется симметричной
относительно прямой 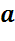 , если для каждой
точки фигуры симметричная ей точка относительно прямой
, если для каждой
точки фигуры симметричная ей точка относительно прямой 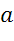 также принадлежит
этой фигуре. Прямая
также принадлежит
этой фигуре. Прямая 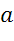 называется осью
симметрии фигуры
называется осью
симметрии фигуры
Фигура называется симметричной
относительно точки 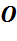 , если
для каждой точки фигуры симметричная ей точка относительно точки
, если
для каждой точки фигуры симметричная ей точка относительно точки 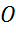 также принадлежит
этой фигуре. Точка
также принадлежит
этой фигуре. Точка 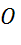 называется
центром симметрии фигуры.
называется
центром симметрии фигуры.
Повторим, что примерами отображения плоскости на себя является осевая и центральная симметрии.
У осевой симметрии есть одно очень важное свойство: осевая симметрия – отображение плоскости на себя, которое сохраняет расстояние между точками.
Пусть точки М и N – какие-нибудь точки плоскости, а точки M1, и N1 – симметричные им точки относительно прямой a. Здесь может быть несколько вариантов расположения точек на плоскости.
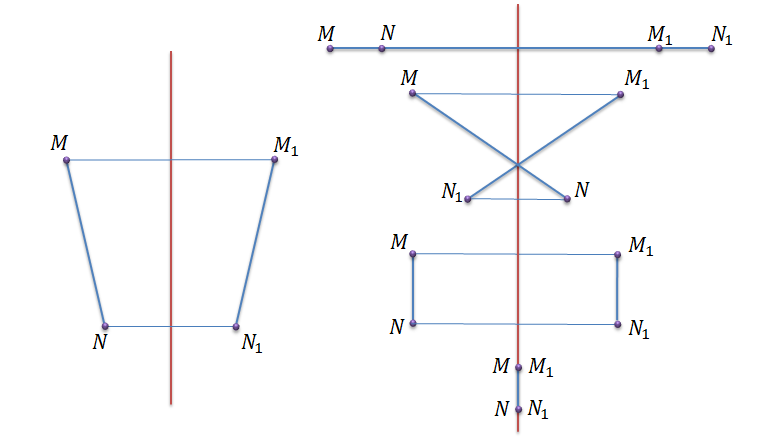
Рассмотрим один из таких вариантов.
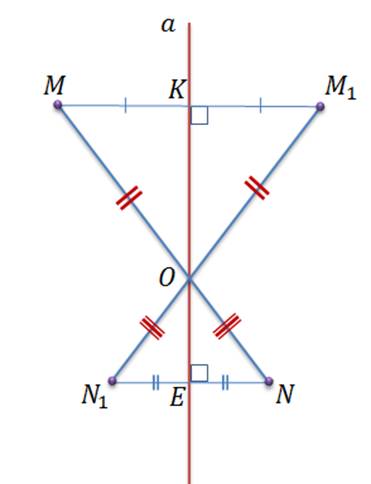
По построению симметричных точек относительно прямой a, прямая a перпендикулярна прямым MM1 и NN1 и делит эти отрезки пополам, значит, в треугольниках МОМ1 и NON1 отрезки ОК и ОЕ будут являться медианами и высотами, проведенными к основанию, то есть это равнобедренные треугольники.
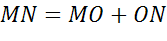 ,
, 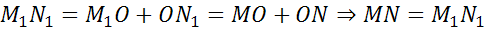
Таким образом, мы доказали, что расстояние между точками М и N равно расстоянию между симметричными им точками M1 и N1. Мы с вами рассмотрели один случай расположения точек. Остальные случаи вы можете рассмотреть самостоятельно и убедитесь, что и в остальных случаях эти расстояния будут равны.
Обобщая, можно сказать, что осевая симметрия является отображением, которое сохраняет расстояние между точками. Любое отображение, обладающее этим свойством, называется движением или по-другому – перемещением.
Давайте сформулируем определение: движение плоскости – это отображение плоскости на себя, сохраняющее расстояния.
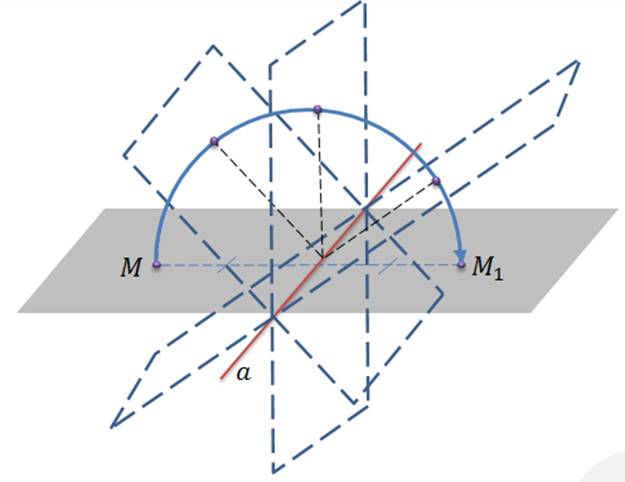
Почему такое отображение называется движением? Если рассмотреть осевую симметрию, то она представляет собой поворот плоскости в пространстве на 180º вокруг оси А.
Нетрудно убедится в том, что центральная симметрия плоскости также является движением.
Рассмотрим точки М и N и точки M1, N1 симметричные точкам М и N относительно точки О.
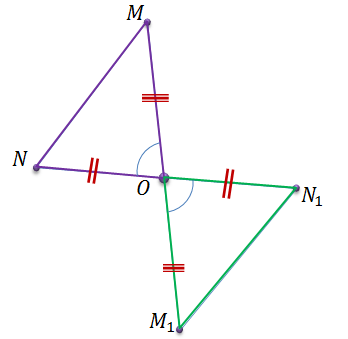
Рассмотрим треугольники MNO и M1ON1.
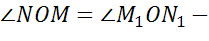 вертикальные
вертикальные
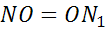
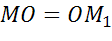
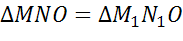
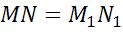
То есть и при центральной симметрии сохраняется расстояние между точками. Тогда по определению движения, получим, что и центральная симметрия является движением.
Теорема. При движении отрезок отображается на отрезок.
Доказательство.
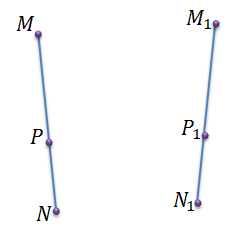
Пусть при некотором движении плоскости концы М и N отрезка MN отображаются в точки M1 и N1. Тогда нам надо доказать, что весь отрезок MN отображается на отрезок M1N1. Возьмем на отрезке МN произвольную точку P. И построим соответствующую ей точку P1.
Поскольку точка P – принадлежит отрезку МN, то можно записать, что
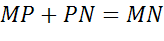 .
.
Поскольку при движении расстояние между точками сохраняется, то
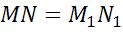
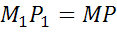
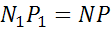
Складывая покомпонентно два последних равенства, получим,
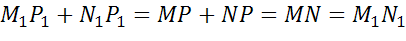
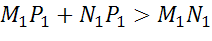
Поскольку точку P на отрезке MN мы выбирали произвольно, то, значит, все точки отрезка MN отображаются в точки отрезка M1N1. Теперь докажем, что в каждую точку P1 отрезка M1N1 отображается какая-нибудь точка P отрезка MN. Пусть точка P1 – произвольная точка отрезка M1N1, и точка P при заданном движении отображается в точку P1.
Тогда из этих соотношений и этого равенства получим,
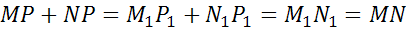
Таким образом, теорема доказана.
Следствие. При движении треугольник отображается на равный ему треугольник.

Доказать это следствие не сложно. Мы доказали, что при движении отрезок отображается в равный ему отрезок. То есть при отображении треугольника мы получим треугольник с равными сторонами, значит, полученный треугольник будет равен исходному по трем сторонам.
Задача. Доказать, что при движении угол отображается на равный ему угол.
Доказательство.
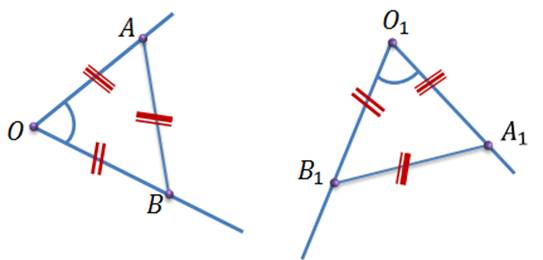
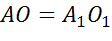 ,
, 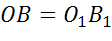 ,
, 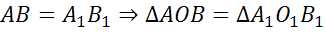
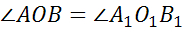
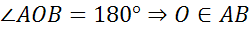
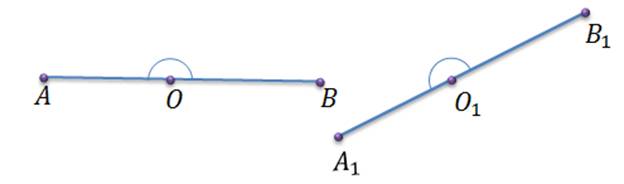
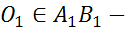 по следствию
по следствию
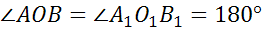
Что и требовалось доказать.
Задача. Доказать, что при движении параллельные прямые отображаются на параллельные прямые.
Доказательство.
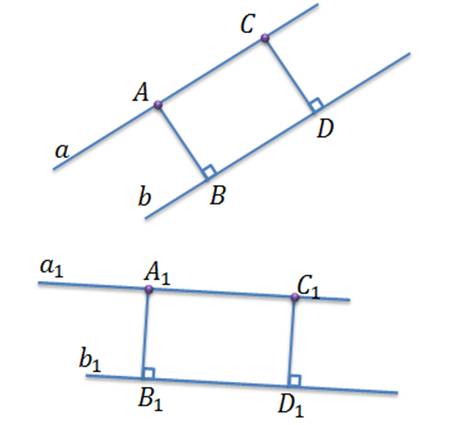
Итак, пусть при некотором движении две параллельные прямые a и b отображаются в прямые a1 и b1. Определим расстояние между параллельными прямыми. Для этого на прямой a возьмем произвольную точку a и проведем перпендикуляр из точки А на прямую b. Длина этого перпендикуляра и будет расстоянием между параллельными прямыми a и b. Мы знаем, что расстояние между параллельными прямыми одинаково, в каком бы месте мы его не измеряли. То есть, если мы измеряем расстояние между прямыми в точке C, то оно будет равно отрезку AB. Отметим на прямых, в которые отобразились прямые a и b точки, соответствующие точкам А, B, C, D. Поскольку расстояния между точками сохраняется при движении, то расстояние между точками А1, B1, C1, D1 будет равно расстоянию между точками А, B, C, D соответственно. То есть расстояния между прямыми, которые получились в результате движения тоже одинаковое, где бы мы это расстояние не мерили, то есть эти прямые параллельны.
Задача. Доказать, что при движении: параллелограмм отображается на параллелограмм, трапеция отображается на трапецию, ромб отображается на ромб, прямоугольник отображается на прямоугольник, а квадрат – на квадрат.
Решение.
Решать эту задачу мы будем, используя предыдущие задачи, теорему и следствие. Мы с вами уже доказали, что равные отрезки отображаются в равные отрезки, параллельные прямые – в параллельные прямые, углы в равные им углы.
Зная все это, решение этой задачи становится очевидным. Поскольку стороны параллелограмма параллельны и равны, то они отобразятся в параллельные и равные отрезки.
Тогда получим, что параллелограмм отобразится в четырехугольник, стороны которого параллельны и равны. А такой четырехугольник является параллелограммом.
Аналогично, поскольку основания трапеции – параллельны, то они отобразятся в параллельные отрезки. Углы трапеции отобразятся в равные им углы, значит, трапеция отобразится в трапецию.
Стороны ромба попарно параллельны и равны, значит, у фигуры, в которую отобразится ромб стороны будут попарно параллельны и равны, то есть ромб отобразится в ромб.
Стороны прямоугольника попарно параллельны и равны, углы между сторонами равны 90º. Значит, при движении прямоугольник отобразится в четырех угольник, стороны которого попарно параллельны, равны, и углы между сторонами равны 90º. То есть прямоугольник отобразится в прямоугольник.
Стороны квадрата попарно параллельны и равны, значит у фигуры, в которую отобразиться квадрат стороны будут попарно параллельны и равны. Углы квадрата равны 90º, значит, и у фигуры, в которую отобразится квадрат углы будут по 90º. То есть фигура в которую отобразится квадрат – это квадрат.
Подведем итоги урока. Итак, на сегодняшнем уроке мы ввели понятие движения. Мы сказали, что движение плоскости – это отображение плоскости на себя, сохраняющее расстояния. Показали, что осевая и центральная симметрии являются движением. Доказали, что отрезок отображается на отрезок, параллельные прямые отображаются в параллельные прямые. Треугольник отображается в треугольник. Угол отображается на равный ему угол.

 Получите свидетельство
Получите свидетельство Вход
Вход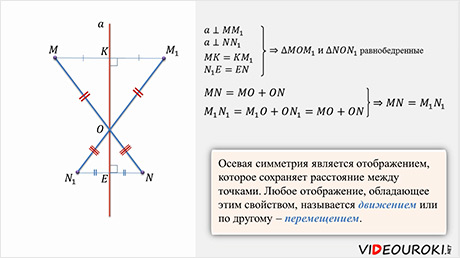



 0
0 13328
13328