Ряд натуральных чисел

Представим себе такую историю…

Раз, два, три, четыре, пять,

Научились мы считать.

Ну а дальше мы не знаем,

Может, вместе посчитаем?

Шесть – конфеты любим есть,

Семь – мы помогаем всем,

Восемь – мы друзей в беде не бросим,

Девять – учимся на пять,

Десять – кончили считать.

Вспоминал считалочку Саша.

– Саша, а что ты делаешь? Для чего это ты считаешь? – спросил Паша.

– Я хочу привести в порядок свою коллекцию солдатиков! Как из них всех выбрать кого-то на первое место? Они же такие все одинаковые! – воскликнул Саша.

– Я совсем не вижу проблемы! Посмотри: на каждом из твоих солдатиков стоит цифра. Ну так и поставь их по порядку! – возразил Паша.

– Как это? Что значит по порядку? – удивился Саша.

– Саша, ты такой смешной! Ты что, в школе не изучал натуральные числа? – с недоумением спросил Паша.

– Какие числа? На-ту-раль-ные??? – ещё больше запутался Саша.

– Да, да, Саша! Именно натуральные! – продолжил Паша. Давай я тебя познакомлю со своим другом Электрошей. И он сейчас тебе всё объяснит.

– Мы каждый день отвечаем на вопрос «Сколько?» – начал Электроша. При этом, помимо слов «много» или «мало», мы называем конкретные числа. Кстати, а вы знаете, что число является основным понятием математики, которое сложилось в ходе очень длительного исторического развития? А чтобы ответить на вопрос «Сколько?», надо сосчитать.

– Вот, Саша, сколько тебе лет? – спросил Электроша.

– Одиннадцать! – уверенно ответил Саша.

– Все те числа, которые вы слышите с самого рождения, и, кстати, они же будут сопровождать вас постоянно и повсюду, помогают нам считать различные предметы и отвечают на вопрос «Сколько?» – продолжал Электроша. –Такие числа называются натуральными.

Запомните! Числа 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 и так далее, используемые при счёте предметов, называют натуральными.

Вот, например, числа 1, 5, 7, 11, 31, 365, 2017, 1 000 000 – это натуральные числа. Но важно понимать, что не все числа, которыми вы пользуетесь, – натуральные. Так, например, числа 0, , , 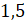– не являются натуральными числами. Об этих числах мы поговорим в другой раз.

Вообще, название «натуральное» происходит от латинского слова natura – ‘природа’. То есть натуральные числа как бы происходят от природы, но, конечно, изобретены они человеческим мозгом.

Впервые термин «натуральное число» появился в трудах римского философа Боэция, жившего ещё в V – VI веках.

– Спасибо, Электроша! – с радостью воскликнул Саша. – Теперь я всё понял и могу с лёгкостью привести в порядок свою коллекцию солдатиков. И тут Саша быстренько начал расставлять солдатиков по своему порядку.

– Саша, ты не всё понял! – остановил Сашу Паша. – Ведь числа тоже имеют свой порядок.

– Порядок? – удивился Саша.

– Да, Саша! Числа тоже хотят жить в порядке! – сказал Электроша.

Если выстроить все числа по порядку, только не просто, как ты сейчас расставил своих солдатиков, а от меньшего числа к большему, то получится натуральный ряд.

Запомните! Все натуральные числа, записанные в порядке возрастания, образуют ряд натуральных чисел (или натуральный ряд).

А вот что тебе ещё нужно знать о натуральном ряде:

1) натуральный ряд чисел начинается с числа 1. То есть первым числом натурального ряда является число 1, вторым – число 2, третьим – число 3 и так далее;

2) в натуральном ряду за каждым числом следует ещё одно число, большее предыдущего на единицу. То есть для того, чтобы получить следующее натуральное число, надо прибавить к текущему натуральному числу единицу;

3) число один не имеет предыдущего. Значит, мы можем с уверенностью говорить, что среди натуральных чисел есть наименьшее число – и это число 1, но нет наибольшего;

4) в натуральном ряду чисел нет последнего числа. Другими словами, натуральный ряд чисел бесконечен, так как к любому числу всегда можно прибавить ещё единицу;

5) натуральных чисел бесконечно много, а вот несуществующих предметов человеку не приходило в голову считать. Поэтому число ноль не натуральное число, так как оно не может получиться в результате счёта;

6) выписать весь натуральный ряд невозможно. Обычно поступают так: выписывают подряд несколько первых чисел натурального ряда, а затем ставят многоточие.

– Вот теперь, Электроша, я точно всё понял – обрадовался Саша. – Посмотри, как я расставил своих солдатиков!

– Да, Саша, на этот раз ты сделал всё правильно! – подбодрил Электроша Сашу. – И раз ты всё понял, предлагаю вам с Пашей закрепить знания на выполнении некоторых заданий.

Задание первое: из указанных чисел выберите натуральные.

11, , 251, 0, 12 800.

Решение: числа 11, 251, 12 800 – натуральные, так как мы их используем при счёте, а вот те числа, которые остались, не будут натуральными.

Следующее задание: из записанных рядов чисел назовите натуральный.

0, 1, 2, 3, 4, 5, 6, 7, …

1, 2, 3, 4, 5, 6, 7, …

7, 6, 5, 4, 3, 2, 1, …

1, 3, 5, 7, 9, 11, …

Решение: в этом задании из всех записанных числовых рядов натуральным будет только второй ряд. Первый ряд не подходит, потому что вначале стоит цифра 0, а мы знаем, что 0 не является натуральным числом. Третий ряд не подходит, так как числа записаны в нём не в порядке возрастания, а в порядке убывания. А вот последний ряд не подходит, потому что в нём каждое последующее число больше предыдущего не на единицу, а на два.

– Саша, Паша, вы отлично справляетесь с заданиями! – с радостью сказал Электроша. – А значит, вы обязательно справитесь с моей непростой задачей.

Задача. 11 коров за 3 дня съедают 33 мешка сена. Сколько мешков сена надо 5 коровам на 5 дней?

Решение: сначала нам нужно найти, сколько мешков сена съедают 11 коров за один день. Для этого 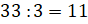 (м.).

Затем мы можем узнать, сколько мешков сена съедает 1 корова за 1 день. Для этого 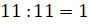 (м.). Получаем, что 1 корова за 1 день съедает 1 мешок сена.

Теперь узнаем, сколько мешков сена съедят 5 коров за 1 день. Для этого 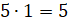 (м.) –– получаем 5 мешков сена.

И осталось выяснить, сколько мешков сена съедят 5 коров за 5 дней. Для этого 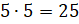 (м.). Получается, что 5 коров за 5 дней съедят 25 мешков сена.