Вопросы занятия:
· рассмотреть правила дифференцирования;
· рассмотреть примеры применения данных правил для нахождения производных функций.
Материал урока.
Прежде чем приступить к изучению новой темы, давайте повторим основные определения:

Для удобства объяснения введём следующие обозначения:
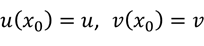
Итак, первое правило помогает нам найти производную суммы двух функций. Производная суммы двух функций есть сумма производных этих функций, другими словами, производная суммы равна сумме производных.
Докажем это свойство.

Для дальнейшего объяснения материала, нам необходимо сформулировать и доказать следующую лемму:
Лемма:

Сформулируем следующее правило: постоянный множитель можно вынести за знак производной.
Это правило доказывается аналогично предыдущему и отдельно рассматривать это доказательство мы не будем.

Сформулируем следующее правило: производная произведения двух функций равна сумме двух слагаемых. Первое слагаемое есть произведение производной первой функции на вторую функцию, а второе слагаемое есть произведение первой функции на производную второй функции.
Докажем это правило.
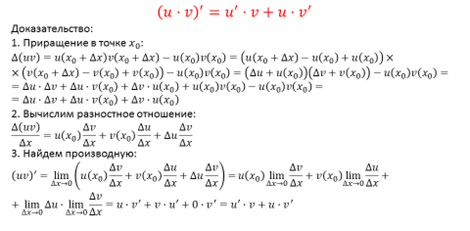
Рассмотрим пример.
Пример.

Сформулируем следующее правило: производная частного двух функций вычисляется по формуле:

Докажем его.


Рассмотрим пример.
Пример.

Докажем, что производная степенной функции xn вычисляется по формуле:


Рассмотрим пример.
Пример.
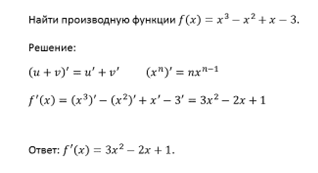
Рассмотрим ещё один пример.
Пример.

Рассмотрим ещё один пример.
Пример.

Итак, повторим основные правила дифференцирования:
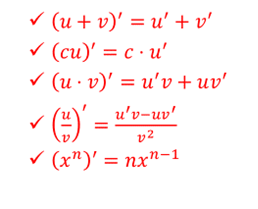

 Получите свидетельство
Получите свидетельство Вход
Вход



 0
0 3967
3967



