Деление рациональных чисел

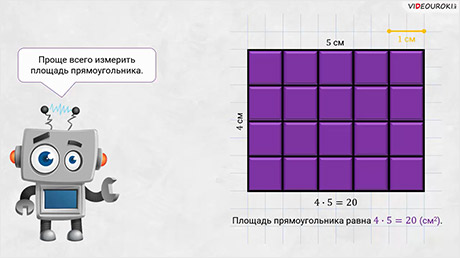
Представим себе такую историю…

– Саша, ты меня звал? – спросил у друга Паша.

– Звал, – ответил Саша. – Помоги мне, пожалуйста, найти среднюю температуру воздуха в выходные. Мама сказала, что если она будет выше нуля, то мы пойдём на прогулку в лес. По прогнозу погоды в субботу должно быть 5 °C мороза, а уже в воскресенье – 1 °C тепла.

 – Мы умеем находить среднее арифметическое нескольких чисел. Для этого мы должны сложить все числа и разделить на их количество, – напомнил другу Паша.

– Тогда мы сложим  и 1 и разделим на 2, – сказал Саша.

– Сумма  и 1 равна , – провёл вычисления Паша. – То есть получается, что нам надо разделить  на 2.

– Но мы не умеем делить отрицательные числа, – с грустью сказал Саша.

– Точно, – сказал Паша и предложил, – давай попросим Мудряша нам помочь.

– Ребята, прежде чем я вам помогу, давайте немного разомнёмся и выполним устные задания, – предложил Мудряш.

– Теперь сверимся! – сказал Мудряш. – Посмотрите, что у вас должно было получиться!

– А сейчас вернёмся к вашему вопросу, – начал Мудряш. – Ребята, вы пока не умеете делить рациональные числа, но знаете, что для натуральных чисел ,  и  верно равенство , если верно равенство . В случае рациональных чисел частное также определяют с помощью умножения.

Запомните! Частным рациональных чисел  и  ()) называют такое рациональное число , произведение которого с числом  равно числу .

То есть , если .

Вернёмся к вашему примеру. Обозначим . Согласно только что сформулированному определению это равенство будет справедливым, если . Несложно заметить, что, умножив  на , мы получаем . То есть .

– Получается, что средняя температура воздуха на выходных будет ниже нуля, а значит, мы с мамой не пойдём на прогулку в лес, – огорчился Саша.

– Таким образом, пользуясь сформулированным определением, можем записать следующие примеры, – продолжил Мудряш.

, так как ;

, так как ;

, так как ;

, так как ;

, так как ;

, так как .

Посмотрите на первый, второй и четвёртый примеры. Здесь мы находим частное двух чисел с разными знаками, – начал Мудряш.

– И в результате получаем отрицательное число, – заметили мальчики.

– Верно! – сказал Мудряш. – Запомните! Чтобы найти частное двух чисел с разными знаками, надо разделить модуль делимого на модуль делителя и поставить перед полученным числом знак «».

В третьем и пятом примерах мы находим частное двух отрицательных чисел.

– И в результате получаем положительное число, – снова заметили Саша и Паша.

– Молодцы! – похвалил ребят Мудряш. – Запомните! Чтобы найти частное двух отрицательных чисел, надо разделить модуль делимого на модуль делителя.

Обратите внимание, что, разделив число на 1, получаем само это число. Частное двух равных чисел равно 1. А деление 0 на рациональное число даёт 0. Запомните! Для любого рационального числа  верно равенство: . Если , то верны равенства: ; . На нуль делить нельзя.

– Паша, Саша, а сейчас давайте выполним несколько заданий, – сказал Мудряш.

Задание первое: выполните деление:

а) ; б) ; в) ; г) ; д) ; е) .

Решение: в первом примере  нам надо разделить отрицательное число на положительное, а значит, мы воспользуемся правилом деления двух чисел с разными знаками. Запишем частное модулей делимого и делителя со знаком «»: . Выполним вычисления и в результате получим .

Во втором примере  также воспользуемся правилом деления двух чисел с разными знаками. Запишем частное модулей делимого и делителя со знаком «»: . Выполним вычисления и в результате получим . Обратите внимание, что при делении на  мы получили число, противоположное делимому.

В третьем примере  снова делим два числа с разными знаками. Запишем частное модулей делимого и делителя со знаком «»: . Заменим деление дробей умножением: . Произведение числителей запишем в числитель, произведение знаменателей запишем в знаменатель: . Сократим на 11. Выполним вычисления и в результате получим .

В четвёртом примере  нам надо найти частное двух отрицательных чисел. Воспользуемся правилом деления двух отрицательных чисел. Запишем частное модулей делимого и делителя: . Выполним вычисления и получим .

В следующем примере  снова делим два отрицательных числа. Запишем частное модулей делимого и делителя: . Заменим деление дробей умножением:  . Произведение числителей запишем в числитель, произведение знаменателей запишем в знаменатель: . Сократим на 3: . Выполним преобразования и в результате получим .

И последний пример . Надо разделить два отрицательных числа. Запишем частное модулей делимого и делителя: . Смешанное число  представим в виде неправильной дроби . Десятичную дробь  заменим обыкновенной дробью . Заменим деление дробей умножением:  . Произведение числителей запишем в числитель, произведение знаменателей запишем в знаменатель: . Сократим на  и на : . Выполним вычисления и в результате получим .

Второе задание: решите уравнение:

а) ; б) ; в) ; г) .

Решение: В первом уравнении нам неизвестен множитель . Мы знаем, чтобы найти неизвестный множитель, надо произведение разделить на известный множитель. Тогда можем записать, что . Воспользуемся правилом деления двух чисел с разными знаками. Запишем частное модулей делимого и делителя со знаком «»: . Выполним деление в скобках. И в результате получим, что .

Второе уравнение. Чтобы найти неизвестный множитель , мы разделим произведение минус  на известный множитель : . Воспользуемся правилом деления двух отрицательных чисел. Тогда икс равняется частному модулей делимого и делителя: . Чтобы разделить  на , перенесём запятую влево на один знак и в результате получим, что .

В следующем уравнении  нам неизвестно делимое. Мы с вами знаем, чтобы найти неизвестное делимое, надо частное умножить на делитель, а значит, . Так как в правой части надо перемножить две дроби с разными знаками, то запишем произведение модулей этих дробей со знаком «»: . Теперь произведение числителей запишем в числитель, произведение знаменателей запишем в знаменатель: . Сократим на 5 и на 4 и в результате получим .

И ещё одно уравнение . Чтобы найти , сначала найдём неизвестный делитель . Мы знаем, чтобы найти неизвестный делитель, надо делимое разделить на частное. Тогда . Чтобы разделить два числа с разными знаками в правой части уравнения, запишем частное модулей делимого и делителя со знаком «»: . Выполним вычисления и получим, что .

Знак «» перед  в левой части уравнения означает, что коэффициент перед  равен : . Теперь, чтобы найти неизвестный множитель , мы разделим произведение  на известный множитель : . Тогда  и .