Вопросы занятия:
· познакомиться с понятием числовой окружности;
· познакомиться со свойствами точек числовой окружности;
· познакомится с точками первого и второго макетов.
Материал урока
Прежде чем приступить к изучению нового материала, давайте повторим понятие числовая прямая.

Давайте выполним упражнение.
Упражнение.

Давайте решим задачу.
Задача.

Определение.
Числовая окружность ̶ модель числовой прямой, на которой можно отметить точку с самой удалённой координатой.

На числовой прямой каждая точка имеет единственное «имя» ̶ число, а на числовой окружности каждая точка может иметь бесконечное множество «имён» ̶ чисел.

Для дальнейшего изучения темы нам пригодятся два макета окружностей.

Рассмотрим несколько примеров.
Пример.

Пример.

Из всех рассмотренных примеров можно вывести и сформулировать следующее утверждение.
Если точка М числовой окружности соответствует числу t, то она соответствует и числу вида t + 2πk, где k – любое целое число (kϵZ).
M(t) = M(t+2πk), где kϵZ
Вернёмся к нашим макетам и, с учётом выше сформулированного утверждения, запишем все точки, отмеченные на макетах.


 Получите свидетельство
Получите свидетельство Вход
Вход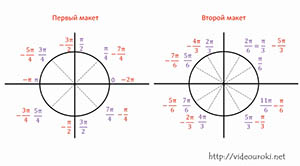



 1
1 9267
9267


спасибо за разработку