Обратная функция

Вопросы занятия:

·     познакомиться с понятиями прямой и обратной функции;

·     познакомиться с понятием обратимой функции;

·     научиться находить обратные функции;

·     рассмотреть свойство обратных функций.

Материал урока

Прежде чем приступить к изучению новой темы, давайте вспомним, что же такое функция и какие основные понятия с ней связаны.

Определение.

Если даны числовое множество X и правило f, которое позволяет поставить в соответствие каждому элементу x из множества X определенное число y, то говорят, что задана функция y=f(x) с областью определения X.

Область определения обозначается D(f).

x – независимая переменная или аргумент.

y – зависимая переменная.

Множество всех значений y=f(x), где x принадлежит множеству X называют областью значений функции и обозначают E(f).

Рассмотрим задачу.

Задача.

Рассмотрим ещё одну задачу.

Задача.

Давайте назовём первую задачу прямой, тогда вторая задача будет обратной к первой.

Давайте рассмотрим с вами ещё одну задачу.

Задача.

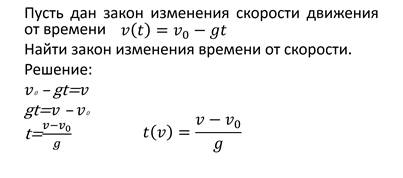
Назовём функцию v(t) обратимой функцией, а t(v) – обратной функцией.

Определение.

Если функция y=f(x) принимает каждое своё значение у только при одном значении x, то эту функцию называют обратимой.

Приведём примеры обратимых функций:

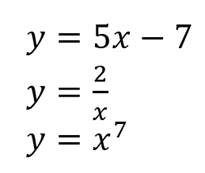
Рассмотрим функцию y=x².

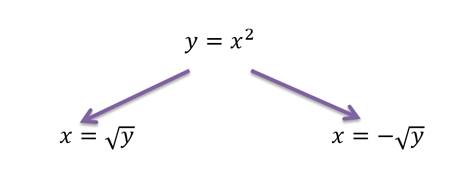
Определение.

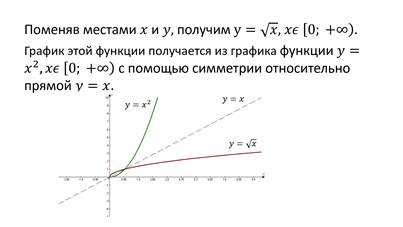
Пусть y = f(x) – обратимая функция. Тогда каждому y из множества значений функции соответствует одно определённое число x из области определения, такое, что f(x) = y. Это соответствие определяет функцию x от y, которую обозначим x = g(y). Поменяем местами x и y: y = g(x). Функцию y = g(x) называют обратной к функции y = f(x). Обозначают f^-1(x).

Давайте разберём это определение на примере.

Пример.

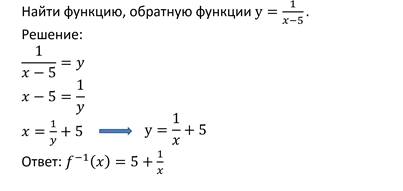
Область определения исходной функции равна области значений обратной функции и наоборот, область значений исходной функции равна области определения обратной функции.

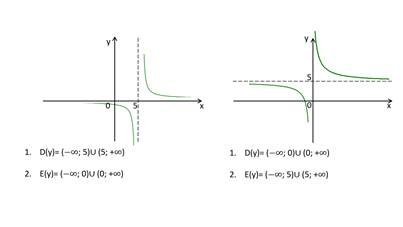
Сформулируем основные свойства обратных функций.

Решим несколько примеров.

Пример.

Пример.