Элементарные функции, их графики и свойства. Часть 1

Вопросы занятия:

·  повторить основные свойства и графики прямой пропорциональности, обратной пропорциональности, линейной функции и функции y=|x|.

Материал урока

И прежде чем мы приступим к повторению свойств элементарных функций, давайте еще раз вспомним основные свойства функций.

К ним относятся: область определения функции, область значений функции, нули функции, промежутки знакопостоянства функции, промежутки монотонности функции. К свойствам мы отнесём ещё и построение графика. Мы это сделали потому, что построив график функции – мы более наглядно можем увидеть основные свойства функции.

И начнём мы с вами с прямой пропорциональности.

Определение.

Прямой пропорциональностью называется функция вида:

1. Областью определения прямой пропорциональности является множество всех действительных чисел.

2. Областью значений является множество всех действительных чисел.

3. Найдём нули функции.

Функция равна нулю при x = 0, то есть нулём функции будет 0.

4. Если k > 0, то функция будет принимать положительные значения при x из промежутка (0; +∞). Отрицательные значения функция будет принимать при x принадлежащих промежутку (-∞; 0).

Если k < 0, то функция принимает положительные значения при x из промежутка (-∞; 0) и отрицательные значения при x из промежутка (0; +∞).

5. При k > 0, функция y = kx возрастает на всей области определения.

При k < 0, функция y = kx убывает на всей области определения.

6. Графиком прямой пропорциональности будет прямая, проходящая через начало координат. Причём, если k > 0, то график функции располагается в I и III координатных четвертях. Если k < 0, то график прямой пропорциональности располагается во II и IV четвертях.

Рассмотрим пример.

Пример.

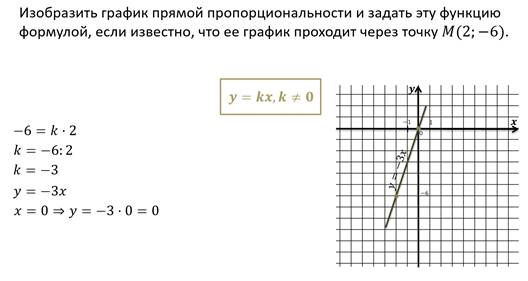
Теперь вспомним основные свойства и график обратной пропорциональности.

Определение.

Функцию, которую можно задать формулой вида:

называют обратной пропорциональностью.

1. Поскольку в обратной пропорциональности переменная находится в знаменателе, то, очевидно, что областью определения обратной пропорциональности будет:

2. Поскольку k ≠ 0, то областью значений обратной пропорциональности является:

3. Поскольку из области значений функции число ноль исключается, то нулей функции нет.

4. Если k > 0, то функция принимает положительные значения при x из промежутка (0; + ∞), отрицательные значения функция принимает при x из промежутка (- ∞; 0).

Если k < 0, то функция принимает положительные значения при x из промежутка (- ∞; 0), отрицательные значения функция будет принимать при x из промежутка (0; + ∞).

5. Если k > 0, то функция убывает на каждом из промежутков области определения.

Если k < 0, то функция возрастает на каждом из промежутков области определения.

6. Графиком обратной пропорциональности является гипербола, которая состоит из двух ветвей. Если k > 0, то ветви гиперболы располагаются в I и III координатных четвертях. Если k < 0, то ветви гиперболы располагаются во II и IV координатных четвертях.

Рассмотрим пример.

Пример.

А теперь поговорим о линейной функции.

Напомним, что линейная функция задаётся формулой y = kx + b, где x – независимая переменная, а k и b – любые действительные числа.

Давайте вспомним основные свойства линейной функции:

1. Областью определения линейной функции является вся числовая прямая.

2. Если k ≠ 0, то областью значений функции является вся числовая прямая. Если же k = 0, то значением функции будет число b. И тогда множество значений функции состоит из одного числа b.

3. Перейдём к нулям функции.

Если k ≠ 0, то функция принимает значение 0 только при:

Если же k = 0, то в случае, когда b ≠ 0, функция не будет иметь нулей, если же b =0, то функция принимает значение ноль при любом x, то есть в этом случае нулём функции будет любое число.

4. Определим промежутки знакопостоянства линейной функции.

5. Если k > 0, то функция возрастает при любых x.

Если k < 0, то функция убывает на всей области определения.

Если k = 0, то перед нами постоянная функция y = b.

6. Мы помним, что графиком линейной функции является прямая. Для построения графика линейной функции достаточно определить координаты двух точек графика и через них провести прямую. Самыми удобными точками являются те точки, в которых либо абсцисса, либо ордината равны нулю.

Рассмотрим пример.

Пример.

Пусть даны две линейные функции:

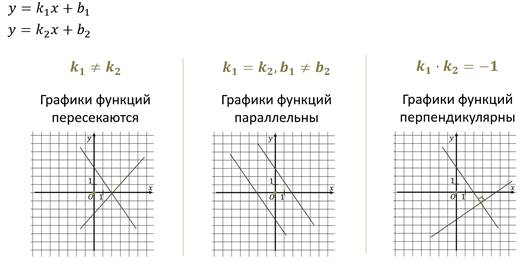
Рассмотрим пример.

Пример.

Теперь давайте повторим основные свойства и график функции y=|x|.

1. Областью определения этой функции будет вся числовая прямая.

2. Поскольку по свойству модуля, модуль может принимать только неотрицательные значения, то область значений функции – интервал [0; + ∞).

3. Найдём нули функции:

4. Определим промежутки знакопостоянства функции:

5. На промежутке [0; +∞) – функция возрастает. На промежутке (-∞; 0] – функция убывает.

6. График функции состоит из двух частей.

Рассмотрим пример.

Пример.

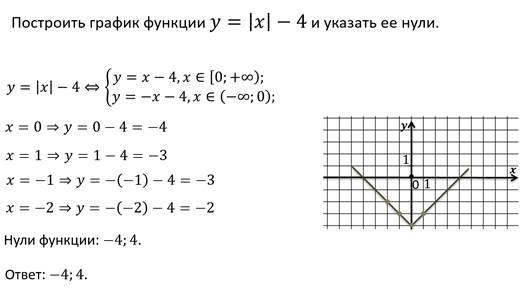
Итоги урока

Сегодня на уроке мы повторили основные свойства и графики прямой пропорциональности, обратной пропорциональности, линейной функции и функции игрек равно модуль икс.