Вопросы занятия:
· вспомнить основные сведения о координатной плоскости, функции;
· повторить основные свойства функции.
Материал урока
Начнём мы с вами с координатной плоскости.
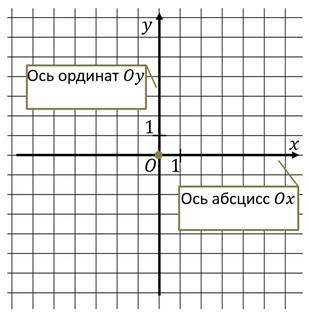
Таким образом, мы задали на плоскости прямоугольную систему координат.
Определение.
Плоскость, на которой задана система координат, называют координатной плоскостью.
Повторим определение функции.
Определение.
Зависимость одной переменной у от переменной х, при которой каждому значению переменной х из определённого множества D соответствует одно определённое значение у, называется функцией от переменной х.
Перед нами графики двух зависимостей.
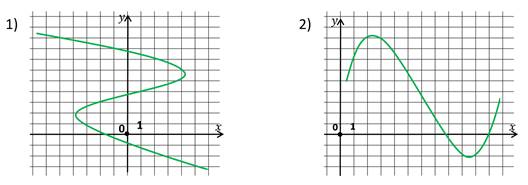
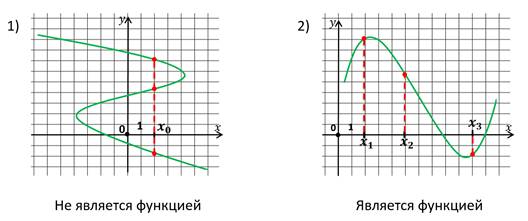
Мы должны определить, какая из них является функцией, а какая нет. В определении сказано, что только та зависимость является функцией, у которой каждому значению аргумента соответствует единственное значение функции. Давайте посмотрим на первый график.
В общем виде любую функцию можно записать так y = f(x). Например, для функции y= 7x – 14 можно записать, что f(x) = 7x – 14, это одно и тоже. Под буквой f понимают некоторый набор действий над переменной x, в данном случае умножение на 7 и вычитание 14.
Переменную x называют независимой или аргументом функции, а y — зависимой (она зависит от x).
Понятно, что функция может принимать различные значения в зависимости от значения аргумента. Найдём значение каждой функции при заданном значении аргумента.

Вы заметили, что в этом задании функции и аргументы названы разными буквами. Действительно, функцию и аргумент можно называть любой буквой латинского или греческого алфавитов.
Сейчас попробуем выяснить, как же получается график функции, и дадим определение этому понятию.
Возьмём, например, функцию y = 7x – 4. Можно записать f(x) = 7x – 4. Это линейная функция, графиком которой, является прямая. Для изображения прямой достаточно двух точек. Найдём значение этой функции, например, при x = 1 и x = -1. Для этого подставим в функцию вместо x сначала 1, затем -1. Тогда получим, что:
f(1) = 7 · 1 – 4 = 7 – 4 =3
Получаем точку с координатами (1; 3).
f(-1) = 7 · (-1) – 4 = -7 – 4 =-11
Получаем точку с координатами (-1; -11).
Проведём прямую через полученные точки. Мы изобразили график функции y = 7x – 4.
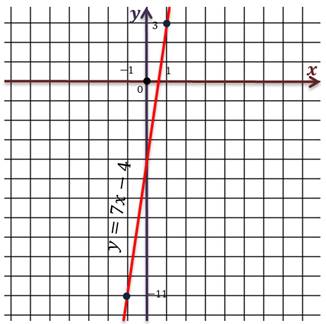
Взяв некоторое x, мы получаем соответствующее y. Эти значения и являются координатами точек графика. Если перебрать все возможные значения x, то мы получим множество точек, изображение которых на координатной плоскости и называют графиком.
Вспомним определение.
Определение.
Множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — значениям функции, называют графиком функции.
Существует три способа задания функции.
Функция может быть задана формулой.
Например, f(x) = 5x + 1.
Функция может быть задана таблицей значений аргумента и функции.
Например,
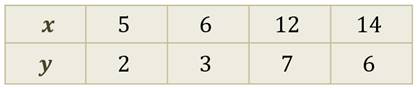
Здесь сразу указаны координаты точек графика функции.
Функция можно задать словесно.
Например, каждому натуральному числу x, из отрезка [10; 20], поставлен в соответствие остаток от деления этого числа на пять. Построить график такой функции не составит труда. Для этого составим таблицу значений аргумента и функции.

Аргументами этой функции будут натуральные числа из отрезка от десяти до двадцати. А значениями функции будут остатки от деления соответствующих аргументов на пять.
Теперь давайте поговорим об основных свойствах функции.
Первое свойство о котором мы поговорим – это область определения.
Все значения аргумента, т.е. переменной x образуют область определения функции (пишут D(f)),
Следующее свойство – область значений функции. Все значения зависимой переменной, т.е. y, — область значений функции (пишут E(f)). В скобках указывают букву, которой названа функция.
Пример.
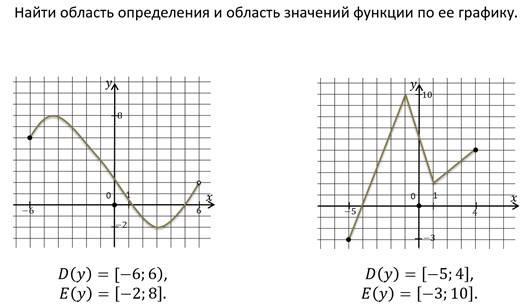
Область определения можно находить не только по графику функции, но и по формуле, с помощью которой задана функция.
Пример.

Следующее свойство, которое мы рассмотрим – нули функции.
Определение.
Значения аргумента, при которых функция принимает значение, равное нулю, называют нулями функции.
Рассмотрим пример.
Пример.
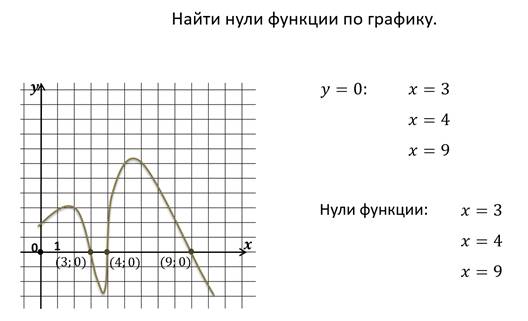
В данном случае функция задана графически и мы определили нули функции по графику. Нули функции можно находить по формуле, с помощью которой задана функция.
Пример.

Стоит обратить внимание на то, что не каждая функция имеет нули.
Например, функция y = x2 + 6.
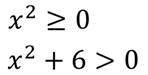
На графике это будет выглядеть так.
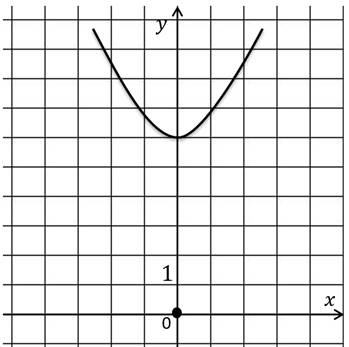
График не пересекает ось икс ни в одной точке.
Теперь поговорим о промежутках знакопостоянства функции.
Определение.
Промежутки знакопостоянства функции — это такие промежутки из области определения, на которых данная функция принимает значения только одного знака, либо положительные, либо отрицательные.
Выполните задание. Запишите промежутки знакопостоянства функции.
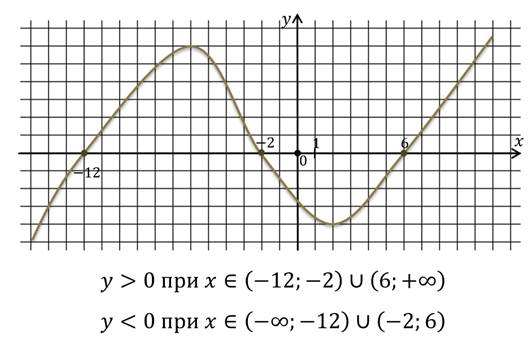
Осталось рассмотреть ещё одно свойство. Промежутки монотонности функции.
Определение.
Функция называется возрастающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции.
Определение.
Функция называется убывающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.
Определение.
Промежутками монотонности называют такие промежутки из области определения, на которых функция либо возрастает, либо убывает.
Пример.
Найдём промежутки монотонности данной функции.
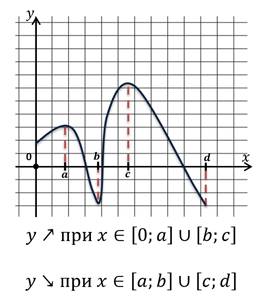
Выполним задание, где нужно описать свойства функции.
Пример.
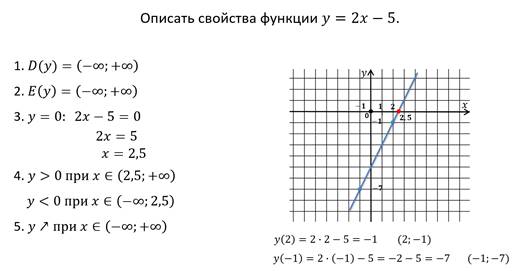
Итоги урока
Сегодня на уроке мы повторили такие понятия как координатная плоскость, функция, график функции, повторили основные свойства функции.

 Получите свидетельство
Получите свидетельство Вход
Вход




 0
0 7534
7534

