Геометрическая прогрессия

Вопросы занятия:

·  повторить основные понятия, связанные с геометрической прогрессии;

·  повторить формулу для нахождения суммы первых n членов геометрической прогрессии;

·  повторить понятие бесконечно убывающей геометрической прогрессии.

Материал урока

Определение.

Геометрической прогрессией называется последовательность отличных от нуля чисел, каждый член которой, начиная со второго, равен предыдущему члену, умноженному на одно и то же число.

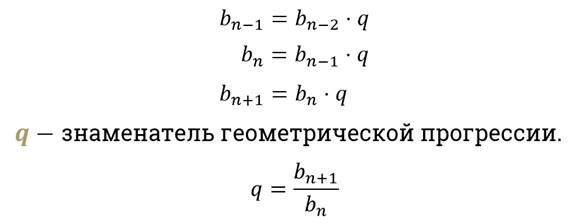
Для задания геометрической прогрессии достаточно задать её первый член и значение знаменателя q.

Рассмотрим пример.

Пример.

Получим формулу n-ого члена геометрической прогрессии.

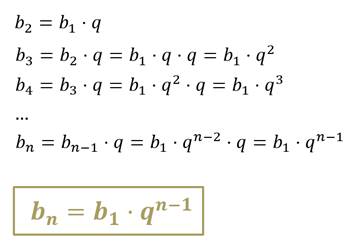
Она позволит найти любой член геометрической прогрессии, зная её первый член и номер искомого члена.

Пример.

Пример.

Пример.

Пример.

Как и в случае просто последовательностей, геометрическая прогрессия бывает возрастающей и убывающей.

Рассмотрим геометрическую прогрессию, состоящую из степеней числа три.

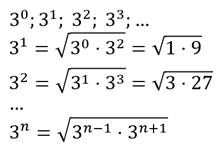
Таким свойством обладает любая геометрическая прогрессия.

Квадрат любого члена геометрической прогрессии, начиная со второго, равен произведению предыдущего и последующего членов.

Другими словами, любой член геометрической прогрессии равен среднему геометрическому предыдущего и последующего членов.

Справедливо и обратное утверждение.

Если в последовательности чисел, отличных от нуля, квадрат каждого члена, начиная со второго, равен произведению предыдущего и последующего членов, то эта последовательность является геометрической прогрессией.

Рассмотрим пример.

Пример.

Рассмотрим пример.

Пример.

Можно сказать, что данная последовательность является геометрической прогрессией.

Рассмотрим геометрическую прогрессию:

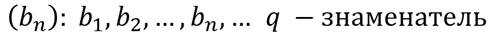
Запишем сумму эн первых членов геометрической прогрессии.

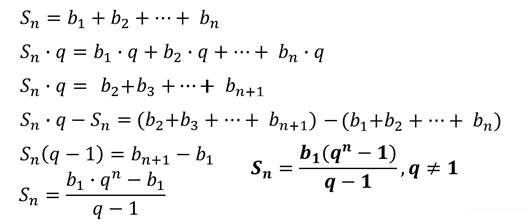
Формулу, записанную в таком виде, на практике использовать удобнее.

Решим несколько примеров.

Пример.

Рассмотрим ещё один пример.

Пример.

Для бесконечно убывающей последовательности сумма первых n членов равна:

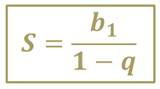
Рассмотрим пример.

Пример.

Итоги урока

Сегодня на уроке, мы повторили основные понятия, связанные с геометрической прогрессией, повторили формулу для нахождения суммы первых эн членов геометрической прогрессии, рассмотрели несколько задач.