Вопросы занятия:
· повторить определение арифметической прогрессии;
· вспомнить свойство арифметической прогрессии;
· вывести формулу для вычисления суммы n первых членов арифметической прогрессии.
Материал урока
Давайте вспомним определение арифметической прогрессии.
Определение.
Арифметическая прогрессия – это числовая последовательность, каждый член которой равен предыдущему, сложенному с одним и тем же числом.
Это число называется разностью арифметической прогрессии.
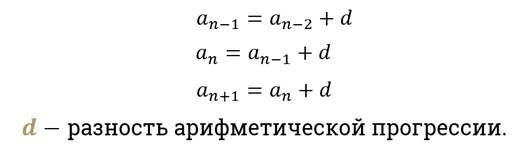
Давайте попробуем среди предложенных последовательностей определить, какие являются арифметической прогрессией, а какие нет.




Пример.

Как и числовые последовательности, арифметические прогрессии бывают возрастающие и убывающие.
Определение.
Возрастающие – это прогрессии, в которых каждый последующий член больше предыдущего.
Например, примерами возрастающих прогрессий будут прогрессии
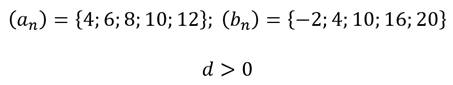
Определить возрастающую арифметическую прогрессию нетрудно, достаточно определить разность прогрессии. Если разность арифметической прогрессии больше нуля, то, значит, арифметическая прогрессия возрастающая.
Определение.
Убывающие арифметические прогрессии – это прогрессии, в которых каждое последующий член меньше предыдущего.
Примерами убывающих прогрессий будут прогрессии
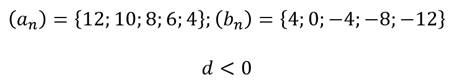
У убывающих арифметических прогрессий – разность арифметической прогрессии меньше нуля.
Рассмотрим пример.
Пример.

Рассмотрим ещё один пример.
Пример.

Теперь давайте рассмотрим задачу.
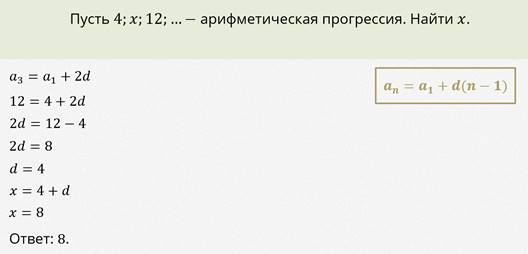
А давайте теперь найдём х, если арифметическая прогрессия такая: 4024; х; 6072?
Вроде тоже ничего сложного, но здесь при вычислении есть шанс сделать вычислительную ошибку.
Давайте решим это задание в общем виде.

Мы с вами сформулировали основное свойство арифметической прогрессии.
Найдём теперь х из предыдущей задачи с помощью только что доказанной формулы.

Теперь давайте выполним задание.
Пример.
Найти сумму первых девяти членов арифметической прогрессии, состоящей из чётных чисел, записанных в порядке возрастания.
Решение.
Восстановить девять членов этой последовательности нетрудно.
Это будут числа: 2; 4; 6; 8; 10; 12; 14; 16; 18.
Их сумма равна: 2 + 4 + 6 + 8 + 10 + 12 + 14 + 16 + 18 = 90.
Ответ: 90.
А если нам надо найти, например, сумму тысячи первых членов? Как быть? Выписывать тысячу членов прогрессии и все их складывать? Это долго и большая вероятность того, что при нахождении всех чисел, мы допустим ошибку, которая повлечёт за собой ошибку при нахождении суммы.
Давайте выведем формулу, которая поможет нам быстро подсчитать сумму сколько угодно членов арифметической прогрессии.

Эта формула, позволяет находить сумму любого количества первых членов арифметической прогрессии, не вычисляя отдельно их значения.
Теперь давайте вернёмся к нашему примеру и посчитаем сумму девяти членов прогрессии по формуле, которую вывели.

Мы получили такой же результат, только нам не пришлось находить все девять членов прогрессии.
Рассмотрим несколько примеров.
Пример.

Рассмотрим ещё один пример.
Пример.

Есть второй способ решения такой задачи.
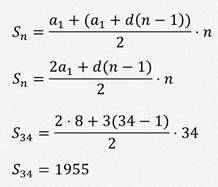
В этом случае, нам не пришлось отдельно вычислять значение тридцать четвёртого члена.
Пример.

Рассмотрим ещё один пример.

Рассмотрим ещё один пример.

Итоги урока
Сегодня на уроке, мы вспомнили определение арифметической прогрессии, повторили свойство арифметической прогрессии, вывели сумму эн первых членов арифметической прогрессии.

 Получите свидетельство
Получите свидетельство Вход
Вход



 0
0 9728
9728

