Сегодня на уроке вы познакомитесь с рациональными числами. Выведите признак, по которому можно объединить все известные вам числа во множество рациональных чисел. А также узнаете, какие дроби называют бесконечными и периодическими.
Числа появились в практической деятельности для подсчёта количества предметов и измерения величин – расстояний, масс, скоростей и т.д.
Они, прежде всего, нужны были для ответа на вопрос «Сколько?».
Например, 5 пальцев, 2 ребёнка, 1 миллион рублей, 2 кг и т.д.

Напомню, такие числа, кроме нуля, называют натуральными числами.
Для тех случаев, когда нужное количество нельзя было выразить натуральным числом, люди придумали дроби – делили целое на несколько равных частей. Тогда ответ на вопрос «сколько» давался в виде некоторого числа таких частей.
Например

Все эти числа, кроме нуля, называются положительными числами.
Например

Перед положительным числом можно поставить знак «+», при этом получается то же самое число.
Однако вскоре поняли, что и положительных чисел не всегда хватает.
Например, чтобы измерить температуру воздуха.

В самом деле, информация о том, что температура воздуха 20°, недостаточна, чтобы правильно выбрать одежду перед выходом на улицу. Необходимо уточнить: 20° тепла или 20° мороза?
Для таких случаев люди придумали так называемые числа со знаком «–». Всем понятно, что 20° мороза обозначаются числом «–20». Таким образом, появились новые числа, которые стали называть отрицательными.
Итак, отрицательные числа – это уже известные нам числа, только со знаком «минус».
Например
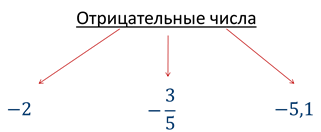
Напомним, что число нуль не относится ни к положительным, ни к отрицательным числам.
Введённые таким образом положительные и отрицательные числа вместе с нулём составляют множество рациональных чисел.
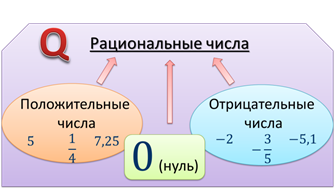
Его принято обозначать заглавной буквой Q.
Теперь давайте попробуем записать эти числа в виде

Любое целое число можно записать в виде обыкновенной дроби, взяв за знаменатель единицу, а за числитель – само это число.
Например
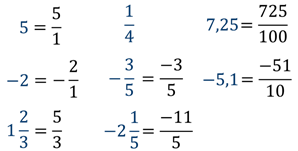
Обратите внимание, все изученные ранее числа, мы
смогли записать в виде отношения  .
.
Определение:
Число, которое можно записать в виде отношения
 ,
где а – целое число, n
– натуральное
число, называют рациональным числом.
,
где а – целое число, n
– натуральное
число, называют рациональным числом.
Сумма, разность и произведение рациональных чисел, тоже рациональные числа.
Например

Если делитель отличен от нуля, то частное двух рациональных чисел тоже рациональное число.
Например

Вы знаете, что обыкновенную дробь можно перевести в десятичную.
Например
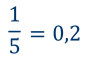
Но оказывается, не все обыкновенные дроби можно представить в таком виде.
Давайте попробуем перевести дробь  в
десятичную.
в
десятичную.

В таком случае пишут бесконечные десятичные дроби:

Читают «нуль целых и три в периоде».
Есть и ещё примеры бесконечных дробей:

Такие записи дробей называют периодическими дробями.
В периодических дробях повторяется одна или несколько цифр.
Повторяющуюся цифру называют периодом.
Сделаем замечание: любое рациональное число можно записать не только в виде обыкновенной дроби, но и в виде десятичной, либо периодической дроби.
На этом уроке мы познакомились с вами с
рациональными числами. Но существуют и другие, не рациональные числа. Одно из
таких чисел вы уже знаете – это число 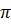 .
Об остальных числах вы узнаете в старших классах.
.
Об остальных числах вы узнаете в старших классах.
Итоги
Число, которое можно записать в виде отношения
 ,
где а – целое число, n
– натуральное число, называют рациональным числом.
,
где а – целое число, n
– натуральное число, называют рациональным числом.
Сумма, разность и произведение рациональных чисел тоже рациональные числа.
Если делитель отличен от нуля, то частное двух рациональных чисел тоже рациональное число.
Любое рациональное число можно записать не только в виде обыкновенной дроби, но и в виде десятичной, либо периодической дроби.

 Получите свидетельство
Получите свидетельство Вход
Вход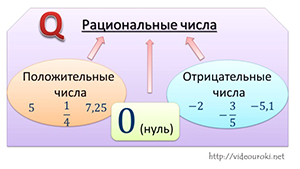



 0
0 8732
8732