Переместительное и сочетательное свойства умножения рациональных чисел. Коэффициент

Представим себе такую историю…

– Саша, чем ты занимаешься? – спросил у друга Паша.

– К следующему уроку математики нам задали решить пример. Он мне кажется сложным, – ответил Саша.

– Покажи мне, – попросил Паша. – Может, я смогу тебе помочь.

– Вот смотри: . Здесь надо перемножить три числа, и для этого придётся потрудиться, – грустно сказал Саша.

– Не расстраивайся. Может, можно как-то упростить эту задачу, – успокоил друга Паша. – А помнишь, на прошлом уроке мы говорили, что для рациональных чисел можно пользоваться переместительным свойством умножения? Тогда, чтобы быстро и легко решить этот пример, мы могли бы поменять местами 25 и , ведь произведение 25 и 4 даёт нам 100.

– А как же быть со скобками, в которые взяты первый и второй множители? – спросил Саша.

– Это хороший вопрос… Интересно, может, для рациональных чисел действует и сочетательное свойство умножения, – задумался Паша.

– Давай спросим у Мудряша, – предложил Саша.

– Давай, – ответил Паша.

– Ребята, прежде чем я отвечу на ваш вопрос, давайте немного разомнёмся и выполним устные задания, – предложил Мудряш.

– Теперь сверимся! – сказал Мудряш. – Посмотрите, что у вас должно было получиться!

– А сейчас вернёмся к вашему вопросу, – начал Мудряш. – Ребята, на прошлом уроке мы с вами сказали, что для рациональных чисел справедливо переместительное свойство умножения. Мы умножили  на 4 и получили . И умножили 4 на  и тоже получили . То есть произведение  и 4 равно произведению 4 и .

У вас возник вопрос, справедливо ли сочетательное свойство умножения для рациональных чисел. Конечно, справедливо. Давайте вернёмся к вашему примеру: . Вы для удобства вычислений поменяли местами первый и второй множители: . Теперь заключим в скобки 25 и 4: . Произведение в скобках равняется 100. Умножим  на 100. Для этого перенесём запятую в десятичной дроби на два знака вправо, так как умножаем на 100, и получим .

Запомните! Для любых рациональных чисел ,  и  справедливы равенства:

 – переместительное свойство умножения;

 – сочетательное свойство умножения.

Теперь с помощью только что рассмотренных свойств умножения упростим вот такое выражение: . Напомним, что в буквенных выражениях знак умножения между буквенными множителями, а также между числовым и буквенным множителями, как правило, не ставится. Запишем вначале все числовые множители и возьмём их в скобки, а затем – буквенные: . Произведение  и  даёт нам . Знаем, что при умножении на  получаем число, противоположное , то есть . Буквенную часть оставим без изменений. Тогда наше выражение принимает вид: . Здесь числовой множитель  называют коэффициентом.

Ребята, посмотрите на следующие выражения: ; ; ; ; ; ; . Назовите их коэффициенты, – предложил Мудряш.

– В выражении  коэффициент равен , – начали мальчики, – в выражении  коэффициент равен , в выражении  коэффициент равен . А в выражении  чему равен коэффициент?

– В этом выражении коэффициент равен , – ответил Мудряш. – Просто он здесь записан после буквенных множителей, а, как правило, его записывают перед буквенными множителями.

– В выражении  коэффициент равен  или ? – снова задали вопрос Саша и Паша.

– В этом выражении ни одно из чисел не является коэффициентом. Чтобы найти здесь коэффициент, надо записать все числовые множители перед буквенными: . Затем перемножить эти числовые множители. Тогда число  будет являться коэффициентом в полученном выражении, – объяснил Мудряш.

– А чему равны коэффициенты в выражениях  и ? – спросили мальчишки.

– Выражение  мы можем с вами записать так: . Поэтому коэффициент здесь равен единице. Выражение  можно записать как , а значит, коэффициент в этом выражении равен .

– Паша, Саша, а сейчас давайте выполним несколько заданий, – сказал Мудряш.

Задание первое: Вычислите:

а) ; б) ; в) .

Решение: в примере  для удобства вычисления воспользуемся сочетательным свойством умножения и заключим в скобки второй и третий множители: . Умножим  на  и получим произведение . Теперь перенесём запятую в десятичной дроби на три знака вправо, так как умножаем на , и в результате получим .

В примере  воспользуемся переместительным свойством умножения и поменяем местами второй и третий множители: . Теперь заключим в скобки первый и второй множители: . Произведение двух отрицательных чисел в скобках равняется произведению модулей этих чисел и равняется 10. Осталось . Для этого перенесём запятую в десятичной дроби на один знак вправо и в результате получим .

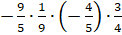Следующий пример . Давайте запишем первый множитель в виде неправильной дроби: . Обратите внимание, что нам будет удобно перемножить  и ,  и . А значит, воспользуемся переместительным свойством умножения и поменяем местами второй и третий множители: . Теперь заключим в скобки первый и второй множители, третий и четвёртый множители: . Перемножим дроби в первых скобках: . Их произведение будет отрицательным, так как они имеют разные знаки. Произведение числителей запишем в числитель, произведение знаменателей запишем в знаменатель: . Сократим на 9, выполним вычисления и получим . Перемножим дроби во вторых скобках: . Их произведение также будет отрицательным, так как они имеют разные знаки. Произведение числителей запишем в числитель, произведение знаменателей запишем в знаменатель: . Сократим на 4, выполним вычисления и получим . Теперь запишем полученные значения в наше выражение: . Произведение двух отрицательных дробей будет положительным. Произведение числителей запишем в числитель, произведение знаменателей запишем в знаменатель: . Сократить мы не можем, поэтому выполним вычисления и получим .

Второе задание: упростите выражение и укажите его коэффициент:

а) ; б) ; в) ; г) .

Решение: в первом выражении  воспользуемся переместительным свойством умножения и поменяем местами второй и третий множители: . Заключим в скобки числовые множители: . Произведение числовых множителей будет положительным, так как они оба отрицательны. Перемножим их и в результате получим . Коэффициентом в полученном выражении является число .

Во втором выражении  воспользуемся переместительным свойством умножения и поменяем местами второй и третий множители: . Заключим в первые скобки числовые множители, во вторые скобки – буквенные множители: . Произведение в первых скобках будет отрицательным, так как множители имеют разные знаки. Перемножим их и получим . Запишем буквенную часть без изменений и в результате получим . Коэффициентом в полученном выражении является число .

В следующем  выражении  также воспользуемся переместительным свойством умножения и поменяем местами второй и третий множители: . В первые скобки заключим первый и второй множители, во вторые скобки – третий и четвёртый множители: . Выполним умножение в первых скобках: . Запишем второй множитель в виде неправильной дроби: . Произведение получится отрицательным, так как множители имеют разные знаки. Произведение числителей запишем в числитель, произведение знаменателей запишем в знаменатель: . Сократим на 3 и на 7. Выполним вычисления и получим . Запишем  в наше выражение, буквенную часть оставим без изменений и в результате получим . Коэффициентом в этом выражении является число .

И последнее выражение . В первую очередь последний множитель  запишем в виде произведения  и : . Воспользуемся переместительным свойством умножения таким образом, чтобы все числовые множители оказались на первом месте, а за ними были буквенные множители: . Заключим в первые скобки все числовые множители, во вторые – все буквенные: . Теперь выполним умножение в первых скобках: . , . Буквенную часть оставим без изменений и в результате получим выражение . Коэффициент в этом выражении равен .