Представим себе такую историю…
– Саша, ты меня звал? – спросил у друга Паша.

– Да, звал. Помоги мне, пожалуйста, разгадать кроссворд. Если мы его разгадаем, то узнаем тему следующего урока математики, – рассказал Саша.
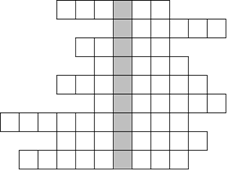
– Хорошо. Давай разгадаем, – согласился Паша.
– Расстояние от начала отсчёта до точки, изображающей данное число на координатной прямой, – зачитал первый вопрос Саша.
– Это расстояние называют модулем, – уверенно сказал Паша.
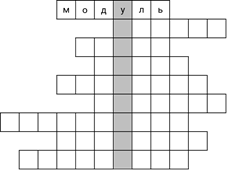
– Точно! Подходит, – записал слово Саша и продолжил, – 60 секунд, слово из 6 букв.
– Наверное, минута, – предположил Паша.
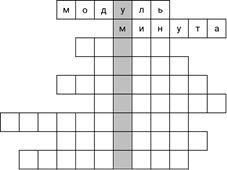
– Подходит, – обрадовался Саша. – Следующее слово – знак действия. 5 букв. Действие сложения обозначают знаком «плюс». Это слово из 4 букв, а значит, не подходит нам. Действие вычитания обозначают знаком «минус». Это слово из 5 букв. Запишем его.
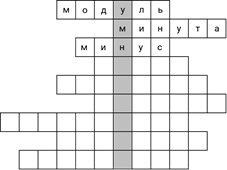
Читаю дальше: отрезок, соединяющий любые две точки окружности. Может, это радиус?
– Посмотри внимательнее. Это слово из 5 букв. А в слове «радиус» 6 букв.
–
Паша, такой отрезок же называют хордой, – радостно сказал Саша и
начал читать следующий вопрос, – действие со знаком «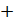 ».
Это действие сложения. Мы сегодня уже вспоминали о нём.
».
Это действие сложения. Мы сегодня уже вспоминали о нём.
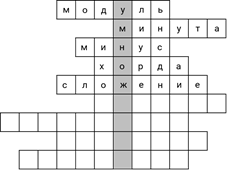
– Верно, – сказал Паша. – Читай дальше.
– Наименьшая единица времени, – продолжил Саша.
– Секунда, – уверенно ответил Паша. – Подходит?
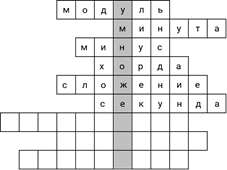
– Подходит, – ответил Саша. – Следующий вопрос. Число, показывающее положение точки на координатной прямой.
– А сколько букв? – cпросил Паша.
– 10 букв, – ответил Саша и сразу же догадался, – так это же координата.
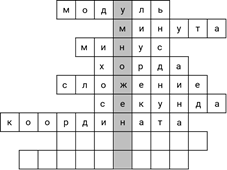
– Читай следующий вопрос, – сказал Паша.
– Сумма длин всех сторон. 8 букв, – зачитал Саша.
– Это периметр, – не задумываясь ответил Паша.
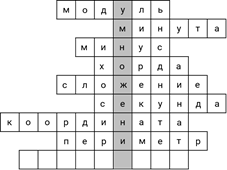
– И осталось разгадать последнее слово, – сказал Саша. – Частное двух чисел, отличных от нуля.
– Это отношение, – сразу догадался Паша.
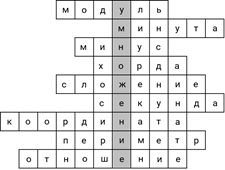
– Кроссворд разгадан, – обрадовался Саша. – И у нас получилось слово «умножение».
– На прошлых уроках мы научились складывать и вычитать рациональные числа, а значит, на следующем уроке будем учиться умножать рациональные числа, – предположил Паша.
– А давай попросим Мудряша рассказать нам об умножении рациональных чисел, – предложил Саша.
– Давай, – согласился с другом Паша.
– Ребята, прежде чем я расскажу вам об умножении рациональных чисел, давайте немного разомнёмся и выполним устные задания, – предложил Мудряш.
– Теперь сверимся! – сказал Мудряш. – Посмотрите, что у вас должно было получиться!

–
А сейчас вернёмся к вашему вопросу, – начал Мудряш. – Ребята, вы знаете, что
умножением называют действие нахождения суммы одинаковых слагаемых. Например, 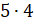 означает
то, что надо найти сумму 4 слагаемых, каждое из
которых равно 5. Это равняется 20.
означает
то, что надо найти сумму 4 слагаемых, каждое из
которых равно 5. Это равняется 20.
Таким
образом, мы произведение 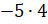 можем
записать в виде суммы 4 слагаемых, каждое из
которых равно
можем
записать в виде суммы 4 слагаемых, каждое из
которых равно 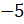 .
А это равняется
.
А это равняется 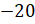 .
.
–
А как тогда записать произведение 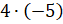 ?
– спросили у Мудряша мальчишки. – Мы же не можем найти сумму
?
– спросили у Мудряша мальчишки. – Мы же не можем найти сумму 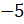 слагаемых.
слагаемых.

– Хороший вопрос! – похвалил ребят Мудряш. – Мы с вами знаем, что для положительных чисел выполняется переместительное свойство умножения.
–
То есть 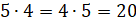 ,
– продолжил Саша.
,
– продолжил Саша.
– Верно! – сказал Мудряш. – Переместительное свойство выполняется и для рациональных чисел.
–
Это значит, что 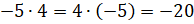 ?
– применил переместительный закон умножения Паша.
?
– применил переместительный закон умножения Паша.
–
Всё правильно, – ответил Мудряш. – При этом обратите внимание, что полученные
произведения 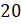 и
и
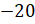 –
противоположные числа, а значит, произведение
–
противоположные числа, а значит, произведение 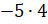 противоположно
произведению
противоположно
произведению 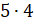 .
Произведение
.
Произведение 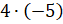 противоположно
произведению
противоположно
произведению 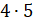 .
То есть можем записать, что
.
То есть можем записать, что 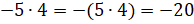 ;
;
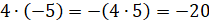 .
.
Посмотрим
на эти равенства и заметим, что произведение чисел с разными знаками равно произведению
модулей этих чисел со знаком «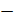 ».
».
При этом обратите внимание, если в произведении отрицательный множитель записан первым, то его не обязательно брать в скобки. Если же отрицательный множитель записан не первым, то брать его в скобки надо обязательно.

Запомните! Чтобы
умножить два числа с разными знаками, надо умножить их модули и
перед полученным произведением поставить знак «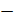 ».
».

– А можно ли умножить два отрицательных числа? – спросили у Мудряша мальчишки.
–
Конечно, можно! – ответил Мудряш. – Давайте найдём произведение 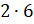 ;
;
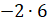 ;
;
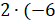 );
);
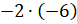 .
Первое произведение равно 12. Второе равно
.
Первое произведение равно 12. Второе равно 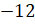 .
Третье – также
.
Третье – также 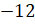 .
Заметим, что при изменении знака одного из множителей в произведении
.
Заметим, что при изменении знака одного из множителей в произведении 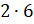 знак
произведения изменился. А если мы изменим знак у каждого из множителей
произведения
знак
произведения изменился. А если мы изменим знак у каждого из множителей
произведения 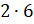 ,
то получается, что знак произведения меняется дважды и в результате остаётся
прежним, то есть
,
то получается, что знак произведения меняется дважды и в результате остаётся
прежним, то есть 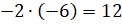 .
Произведение модулей
.
Произведение модулей 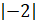 и
и
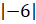 также
даёт
также
даёт 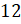 .
.

Поэтому можем сформулировать правило.
Запомните! Чтобы умножить два отрицательных числа, надо умножить их модули.

–
Давайте с вами решим несколько примеров. Первый пример 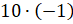 .
.
–
Здесь нам надо найти произведение двух чисел с разными знаками, – подсказал
Мудряшу Саша. – Для этого мы должны умножить их модули и перед произведением
поставить знак «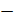 »:
»: 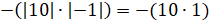 . И
у нас получится
. И
у нас получится 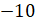 .
.
–
Верно! – сказал Мудряш. – Второй пример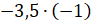 .
.
–
Нам надо найти произведение двух отрицательных чисел. Для этого мы просто
перемножим модули множителей: 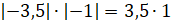 . И
получим
. И
получим 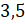 ,
– решили пример мальчики.
,
– решили пример мальчики.
–
В третьем примере 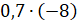 запишем
произведение модулей множителей со знаком «
запишем
произведение модулей множителей со знаком «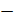 »,
так как находим произведение двух чисел с разными знаками:
»,
так как находим произведение двух чисел с разными знаками: 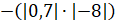 ,
– начал Мудряш.
,
– начал Мудряш.
–
И, выполнив вычисления, получим 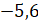 ,
– помогли ему мальчишки.
,
– помогли ему мальчишки.
–
Молодцы! – похвалил Мудряш Сашу и Пашу. – Следующий пример:
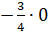 .
.
– Это равно 0, – уверенно сказали ребята, – ведь умножение на 0 всегда даёт 0.
–
Совершенно верно! – сказал Мудряш. – В следующем примере нам надо 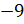 умножить
на
умножить
на 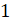 .
.
– Раньше при умножении на 1 мы всегда получали то же самое число, – сказал Саша.
–
Верно! – сказал Мудряш. – Запишем произведение модулей множителей со знаком «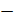 »:
»: 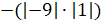 .
И, выполнив вычисления, получим
.
И, выполнив вычисления, получим 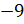 .
И последний пример:
.
И последний пример: 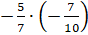 .
Произведение этих отрицательных дробей будет равно произведению их модулей, то
есть нам надо умножить
.
Произведение этих отрицательных дробей будет равно произведению их модулей, то
есть нам надо умножить  на
на
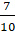 .
.
–
Для этого мы произведение числителей запишем в числитель, произведение
знаменателей запишем в знаменатель: 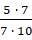 .
Сократим дробь на 5 и на 7
и получим
.
Сократим дробь на 5 и на 7
и получим  ,
– провели вычисления Саша и Паша.
,
– провели вычисления Саша и Паша.

–
Ребята, а теперь давайте внимательно посмотрим на эти примеры, – сказал Мудряш.
– В первом и втором примерах мы умножали числа на 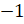 и
получали противоположные им. А значит, можем сказать, что при умножении числа
на
и
получали противоположные им. А значит, можем сказать, что при умножении числа
на 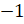 получаем
число, противоположное данному.
получаем
число, противоположное данному.
В четвёртом примере умножали на 0 и получили 0. В пятом примере умножали число на 1 и получили само это число.
В третьем примере умножали два числа с разными знаками и получили отрицательное произведение. А в шестом умножали два отрицательных числа, то есть с одинаковыми знаками, и получили положительное произведение.
Сделаем
из этого следующие выводы. Запомните! Для любого рационального числа a
верны равенства: 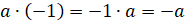 ;
;
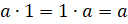 .
.
Если
числа a и b
имеют одинаковые знаки, то произведение 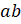 положительно.
И наоборот, если произведение
положительно.
И наоборот, если произведение 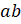 положительно,
то числа a и b
имеют одинаковые знаки.
положительно,
то числа a и b
имеют одинаковые знаки.
Если
числа a и b
имеют разные знаки, то произведение 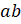 отрицательно.
И наоборот, если произведение
отрицательно.
И наоборот, если произведение 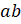 отрицательно,
то числа a и b
имеют разные знаки.
отрицательно,
то числа a и b
имеют разные знаки.
Если
хотя бы одно из чисел a
или b равно нулю, то
произведение 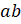 равно
нулю. И наоборот, если произведение
равно
нулю. И наоборот, если произведение 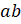 равно
нулю, то хотя бы одно из чисел a
или b равно нулю.
равно
нулю, то хотя бы одно из чисел a
или b равно нулю.



–
Ребята, прежде чем закрепить умение умножать рациональные числа, давайте с вами
рассмотрим выражение 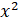 .
Мы знаем, что
.
Мы знаем, что 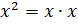 .
Если
.
Если 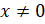 ,
то это является произведением двух равных чисел, а значит, чисел с одинаковыми
знаками. А мы только что сказали, что произведение чисел с одинаковыми знаками
положительно, то есть
,
то это является произведением двух равных чисел, а значит, чисел с одинаковыми
знаками. А мы только что сказали, что произведение чисел с одинаковыми знаками
положительно, то есть 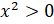 .
.
Если
же 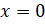 ,
то
,
то 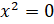 .
Таким образом, выражение
.
Таким образом, выражение 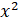 принимает
только неотрицательные значения.
принимает
только неотрицательные значения.
Запомните!
При
любых значениях 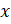 выражение
выражение
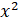 принимает
только неотрицательные значения, то есть
принимает
только неотрицательные значения, то есть 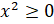 .
.

– Паша, Саша, а сейчас давайте выполним задание, – сказал Мудряш.
Выполните умножение:
а)
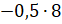 ;
б)
;
б) 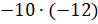 ;
в)
;
в) 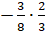 ;
г)
;
г) 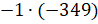 ;
д)
;
д) 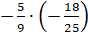 ;
е)
;
е) 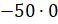 .
.
Решение: В
первом примере 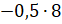 нам
надо умножить отрицательное число на положительное. Воспользуемся правилом
умножения двух чисел с разными знаками. Тогда запишем произведение модулей
множителей со знаком «
нам
надо умножить отрицательное число на положительное. Воспользуемся правилом
умножения двух чисел с разными знаками. Тогда запишем произведение модулей
множителей со знаком «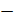 »:
»: 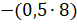 . И, выполнив умножение в
скобках, получим
. И, выполнив умножение в
скобках, получим 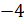 .
.
Второй
пример: 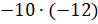 . Воспользуемся
правилом умножения двух отрицательных чисел. Тогда перемножив
. Воспользуемся
правилом умножения двух отрицательных чисел. Тогда перемножив 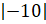 и
и
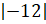 ,
то есть
,
то есть 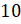 и
и
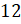 ,
получим
,
получим 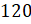 .
.
В
третьем примере 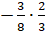 воспользуемся
правилом умножения двух чисел с разными знаками. Запишем произведение модулей
дробей со знаком «
воспользуемся
правилом умножения двух чисел с разными знаками. Запишем произведение модулей
дробей со знаком «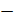 »:
»: 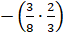 . Перемножим
дроби в скобках. Произведение числителей запишем в числитель, произведение знаменателей
запишем в знаменатель:
. Перемножим
дроби в скобках. Произведение числителей запишем в числитель, произведение знаменателей
запишем в знаменатель: 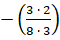 . Сократим
на 3
и
на 2
и получим
. Сократим
на 3
и
на 2
и получим 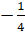 .
.
Четвёртый
пример: 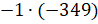 .
Мы с вами уже знаем, что при умножении числа на
.
Мы с вами уже знаем, что при умножении числа на 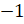 получаем
число, противоположное данному. А значит,
получаем
число, противоположное данному. А значит, 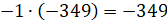 .
.
В
следующем примере 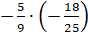 нам
надо перемножить две отрицательные дроби. Воспользуемся правилом умножения двух
отрицательных чисел. Запишем произведение модулей этих дробей:
нам
надо перемножить две отрицательные дроби. Воспользуемся правилом умножения двух
отрицательных чисел. Запишем произведение модулей этих дробей: 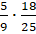 .
Произведение их числителей запишем в числитель, произведение их знаменателей
запишем в знаменатель:
.
Произведение их числителей запишем в числитель, произведение их знаменателей
запишем в знаменатель: 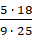 .
Сократим на 5 и на 9
и получим
.
Сократим на 5 и на 9
и получим  .
.
В
последнем примере 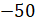 умножаем
0
и получаем 0, так как если хотя бы один из множителей
равен 0,
то и произведение равно 0.
умножаем
0
и получаем 0, так как если хотя бы один из множителей
равен 0,
то и произведение равно 0.


 Получите свидетельство
Получите свидетельство Вход
Вход



 1
1 4590
4590


Внимательно просмотрите видео