Наверняка, в физике, биологии, химии или географии вы сталкивались, как с очень большими, так и очень малыми положительными числами.
Например

Скажите с такими числами удобно выполнять математические расчёты? Конечно же, нет. В обычном десятичном виде большие и малые числа неудобно читать и записывать, неудобно выполнять над ними какие-либо действия. В таком случае полезным оказывается представление числа в виде

Например:

Тогда
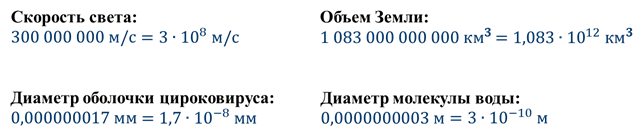
Говорят, что мы записали числа в стандартном виде. В таком виде можно представить любое положительное число.
Определение:
Стандартным видом числа  называют его
запись в виде:
называют его
запись в виде: 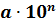 , где
, где 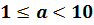 и
и
 –
целое число.
–
целое число.
Число  называется
порядком числа
называется
порядком числа  .
.
Например
Если порядок числа  равен
равен 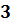 , то это означает,
что
, то это означает,
что 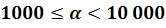 .
.
Если порядок числа  равен
равен 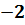 , то это означает,
что
, то это означает,
что 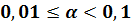 .
.
Большой положительный порядок показывает, что число очень велико.
Большой по модулю отрицательный порядок показывает, что число очень мало.
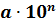 , где
, где 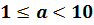 и
и  – целое число
– целое число
По определению стандартного вида числа следует, что в стандартном виде в целой части числа (до запятой) может содержаться только одна цифра.
Все остальные цифры должны стоять после (справа) от запятой.
Порядок числа даёт представление о том, насколько велико или мало это число.
В стандартном виде можно записать не только большое или малое, но и любое число.
Для того чтобы привести число к стандартному виду, надо:
1. Перенести в нём запятую так, чтобы она была сразу после первой значащей цифры.
2.
полученное число умножить на 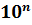 , где
, где  подбирается так, чтобы произведение было равно
данному числу.
подбирается так, чтобы произведение было равно
данному числу.
Значащей цифрой числа называют его первую (слева направо) отличную от нуля цифру, а также все последующие за ней цифры.
Пример: представим в стандартном виде число.
Решение:

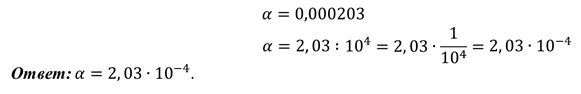
Задание: запишите число в стандартном виде.
Решение:

Задание: запишите в стандартном виде число, равное значению произведения х и у.
Решение:

Итоги:
Стандартным видом числа 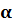 называют его запись
в виде:
называют его запись
в виде: 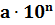 , где
, где 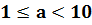 и
и 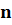 – целое число.
– целое число.
Число
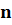 называется порядком числа
называется порядком числа 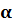 .
.
Для
того, чтобы привести число к стандартному виду, надо перенести в нём
запятую так, чтобы она была сразу после первой значащей цифры, и полученное
число умножить на 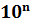 , где
, где 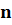 подбирается так, чтобы произведение было равно
данному числу.
подбирается так, чтобы произведение было равно
данному числу.

 Получите свидетельство
Получите свидетельство Вход
Вход



 0
0 15197
15197