Сбор и группировка статистических данных

Ещё в курсе алгебры 7 класса мы с вами познакомились с некоторыми из характеристик статистики.

Напомним, что статистика это один из разделов математики. Она помогает нам накапливать и анализировать информацию, делать выводы, планировать результат.

Само слово статистика происходит от латинского «статус», означающего «состояние дел».

Определение:

Статистика – это наука, которая занимается получением, обработкой и анализом количественных данных о разнообразных массовых явлениях, происходящих в обществе и природе.

Пусть, например, на концерт одной известной группы было продано 2000 билетов. Участники группы решили выяснить кого больше среди почитателей их музыки: мужчин или женщин.

Конечно, определить количество тех или иных будет очень сложно. И тут нам на помощь приходит статистика. В тех случаях, когда бывает сложно или даже невозможно провести полное исследование, его заменяют выборочным. Т.е. если известно, что среди 50 посетивших концерт было 40 мужчин и 10 женщин, то можно сделать вывод, что среди всех 2000 купивших билеты, мужчин было больше.

В таких случаях, множество всех объектов, или в нашем случае, множество всех зрителей, называется генеральной совокупностью.

А та часть объектов, которая выбирается для исследования, называется выборочной совокупностью, или выборкой. В нашем случае – это те 50 человек, пол которых мы точно знаем. При этом выборка должна быть представительной, или, как говорят, репрезентативной, т.е. достаточной по объему и отражающей характерные особенности исследуемой генеральной совокупности.

Для обобщения и систематизации данных, полученных в ходе статистического наблюдения, их по какому-либо признаку разбивают на группы и результаты, характеризующие каждую группу, сводят в таблицы.

Пример, в конце учебного года провели контрольный срез по математике. В ходе проверки теста получили следующие результаты: «двойку» получили 3 ученика, «тройку» - 6 учеников, «четвёрку» - 11 учеников и «пятёрку» - 7 учеников.

Эти данные можно свести в таблицу.

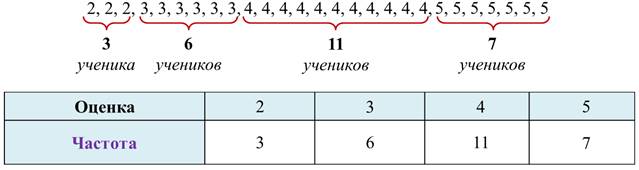
Заметим, что в нижней строке таблицы указывается количество учеников, получивших ту или иную оценку. Или иными словами, указывается частота появления этого числа в общем ряду полученных оценок.

Такую таблицу называют таблицей частот.

Давайте проведём анализ полученных данных.

Иногда в таблице для каждого данного указывают не частоту, а отношение частоты к общему числу данных в ряду. Это число, выраженное в процентах, называют относительной частотой, а саму таблицу – таблицей относительных частот.

Для нашего примера таблица относительных частот выглядит так:

Нетрудно убедиться, что в данном случае сумма относительных частот составляет 100%. Вообще сумма относительных частот, полученных в результате любого исследования, равна 100%.

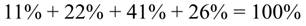
Заметим, что если в ряду имеется большое число данных и одинаковые значения встречаются редко, то таблицы частот или относительных частот теряют наглядность и становятся излишне громоздкими. В таких случаях для анализа данных строят интервальный ряд.

Для этого разность между наибольшим и наименьшим значениями делят на несколько равных частей и, округляя полученный результат, определяют длину интервала. За начало первого интервала часто выбирают наименьшее данное или ближайшее к нему целое число, не превосходящее его. Для каждого интервала указывают число данных попадающих в этот интервал. При этом граничное число считают относящимся к следующему интервалу.

Пример. В магазине выясняли возраст потребителей йогурта. По результатам опроса 100 человек была составлена следующая таблица распределения потребителей йогурта по возрасту.

Пользуясь составленной таблицей, найдём средний возраст, потребителей йогурта. Для этого составим новую таблицу частот, заменив каждый интервал числом, которое является его серединой.

Итоги:

На этом уроке мы узнали, что множество всех исследуемых объектов называют генеральной совокупностью. А та часть объектов, которая выбирается для исследования, называется выборочной совокупностью, или выборкой. Познакомились с таблицами частот и относительных частот. Провели анализ данных на конкретном примере, и вспомнили такие статистические характеристики, как среднее арифметическое, размах, мода и медиана. А также узнали, для чего строят интервальные ряды и научились с ними работать.