При изучении физики в восьмом классе мы говорили о том, что изменить состояние термодинамической системы, то есть её внутреннюю энергию, можно двумя способами: используя теплопередачу или совершая механическую работу. Поговорим о последней более подробно.
Итак, когда мы изучали механику, мы с вами говорили о том, что работа силы (то есть механическая работа) связана с превращением одного вида энергии в другой, например, механической энергии во внутреннюю. При этом работу силы мы рассматривали как меру изменения энергии физической системы.
А вот как определить работу в термодинамике, ведь при рассмотрении термодинамических процессов механическое перемещение макротел в целом не рассматривается?
Забавно, но работа в термодинамике определяется так же, как и в механике, но она равна изменению не механической энергии тела, а изменению его внутренней энергии.
Итак, давайте рассмотрим газ, находящийся в цилиндрическом сосуде с площадью основания S, и закрытый подвижным поршнем. Взаимодействие газа с поршнем, а также со стенками сосуда можно характеризовать давлением, которое газ оказывает на них.
Начнём медленно нагревать газ так, чтобы его давление не изменялось. Очевидно, что в этом случае газ будет изобарически расширяться, а поршень начнёт перемещаться за счёт работы силы давления газа над внешними телами.

Предположим, что поршень переместился на расстояние ∆l. Так как в процессе расширения давление газа не изменялось, то и сила давления газа на поршень оставалась неизменной:
F = pS.
Поэтому работу этой силы мы можем найти как произведение модуля силы на модуль перемещения и на косинус угла между направлением вектора силы и вектора перемещения (в нашем примере правда, этот угол равен нулю):

Подставим в записанное уравнение выражение для силы давления:

А теперь давайте подумаем, что определяет произведение площади основания сосуда (она же площадь основания поршня) и модуля перемещения поршня?.. Да, оно определяет приращение объёма:

Тогда работа газа при его изобарном расширении будет определяться произведением давления газа на изменение его объёма:

Из этой формулы следует, что сила давления газа совершает работу только в процессе изменения объёма газа.
А так как давление газа всегда величина положительная, то из формулы также следует, что при расширении газ совершает положительную работу. При сжатии же газа сила давления будет совершать отрицательную работу.
Процесс медленного изобарного сжатия газа можно характеризовать и работой внешних сил над газом, которая отличается от работы самого газа только знаком:

А теперь давайте запишем уравнение Клайперона — Менделеева для двух состояний газа в цилиндре:

И вычтем из второго уравнение первое:

В левой части полученного равенства у нас стоит произведение давления газа на изменение его объёма. А это, как мы с вами нашли ранее, есть не что иное, как работа газа при изобарном процессе:

Теперь предположим, что в сосуде под поршнем находится один моль идеального газа и в результате изобарного расширения его температура изменилась на один кельвин. Тогда получим, что «А равно Эр»:

Отсюда вытекает физический смысл универсальной газовой постоянной: она численно равна работе, совершаемой одним молем идеального газа при его изобарном нагревании на один кельвин.
Работе газа при его изобарном расширении или сжатии можно дать простое геометрическое токование. Для этого давайте построим график зависимости давления газа от занимаемого им объёма. Очевидно, что графиком является прямая линия, параллельная оси абсцисс.

А площадь прямоугольника, ограниченного графиком процесса, осью V и прямыми, соответствующими значениям объёмов в начальном и конечном состояниях газа, — это есть ничто иное, как работа газа.
Если процесс перехода газа из начального состояния в конечное не является изобарным, то кривую зависимости давления газа от занимаемого им объёма можно представить как ломаную, состоящую из большого числа изохор и изобар. Работа на изохорных участках равна нулю, а суммарная работа на всех изобарных участках будет равна площади заштрихованной фигуры.

А теперь для закрепления материала решим с вами несколько классических задач. В первой задаче нам необходимо будет определить работу, совершаемую силой давления идеального газа определённой массы при его изобарном нагревании от 290 К до 355 К, если давление газа и его начальный объём соответственно 200 кПа и 0,1 м3.

Задача 2. Идеальный газ в количестве 3 молей находится при температуре 350 К. После изохорного охлаждения, в результате которого давление уменьшилось в два раза, газ испытывает изобарное расширение, причём в конечном состоянии температура равна первоначальной. Изобразите графически эти процессы в осях p, V и вычислите совершённую газом работу.


 Получите свидетельство
Получите свидетельство Вход
Вход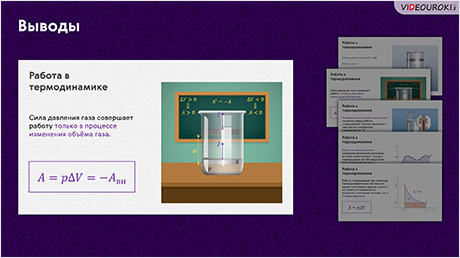




 9515
9515