Внутренняя энергия

Прежде чем приступить к изучению нового материала, давайте с вами вспомним, чем мы занимались при изучении молекулярно-кинетической теории. Там наша основная задача заключалась в установлении связи между макроскопическими параметрами, характеризующими состояние системы, и её микроскопическими параметрами. Это позволило нам объяснить, почему газ оказывает давление на стенки сосуда, что такое температура и так далее.

Также мы с вами вывели уравнение состояния идеального газа. Удалось нам это сделать только потому, что мы рассматривали самую простую систему — идеальный газ. Напомним, что в идеальном газе отсутствуют взаимодействия между молекулами, и поэтому нам не нужно было учитывать потенциальную энергию их взаимодействия. Однако, если бы мы попытались построить молекулярно-кинетическую теорию реального газа (не говоря уже о жидкостях и твёрдых телах), то всё было бы гораздо сложнее, а порой и почти невозможно.

Но существует ещё один раздел молекулярной физики, который пытается установить соответствия между макроскопическими параметрами, абсолютно не интересуясь, как устроена система (то есть без учёта молекулярного строения тел). Этот раздел физики называется термодинамикой.

Интересно, что первой научной теорией тепловых процессов была не молекулярная физика, а именно термодинамика. Считается, что она берёт своё начало с работы Сади Карно «О движущей силе огня и о машинах, способных развивать эту силу», опубликованной в 1824 году.

А становление термодинамики как науки началось примерно в 40-х годах XIX века после того, как Юлиус Майер, Герман Гельмгольц и Джеймс Джоуль количественно определили связь между механической работой и теплотой и сформулировали универсальный закон сохранения и превращения энергии.

Выводы термодинамики основаны на фундаментальных законах, называемых началами термодинамики. Это не теоретические законы. Все они были установлены в результате обобщения многочисленных экспериментальных фактов.

Все физические тела и их модели в термодинамике мы будем называть термодинамическими системами.  При этом для каждой изолированной термодинамической системы существует состояние термодинамического равновесия, в которое она переходит самопроизвольно. Это утверждение называют нулевым началом термодинамики.

Основным понятием в термодинамике является понятие внутренней энергии, о которой мы говорили ещё в восьмом классе. Давайте с вами вспомним, что под внутренней энергией тела (или системы тел) понимают сумму кинетической энергии хаотического теплового движения молекул и потенциальной энергии их взаимодействия.

Обозначают внутреннюю энергию большой латинской буквой U. А измеряют её в тех же единицах, что и механическую энергию, то есть в джоулях.

[U] = [Дж].

Теперь давайте с вами вспомним, от каких величин зависит внутренняя энергия тела или системы тел. Мы уже с вами знаем, что чем выше температура тела, тем быстрее движутся его молекулы и тем больше их кинетическая энергия. Значит, внутренняя энергия тела зависит от его температуры.

Также нам известно, что для перевода вещества, например, из жидкого состояния в газообразное, нужно к веществу подвести энергию. Следовательно, пар будет обладать большей внутренней энергией, чем жидкость той же массы. Значит, внутренняя энергия тела при неизменной массе зависит от его агрегатного состояния.

Ну а так как масса тела равна сумме масс составляющих его частиц, то внутренняя энергия зависит и от массы тела.

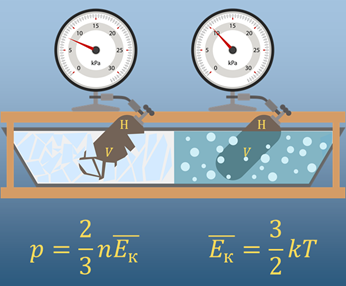
Но внутренняя энергия тела не зависит от его механического движения и от его взаимодействия с другими телами. Так, например, внутренняя энергия мяча, лежащего на полу и поднятого на некоторую высоту от пола, одинакова, так же как и мяча, неподвижного и катящегося по полу (если, конечно, пренебречь силами сопротивления его движению).

Рассчитать внутреннюю энергию можно только для идеального газа. Давайте с вами определим внутреннюю энергию идеального одноатомного газа, то есть газа, состоящего из отдельных атомов (к такому газу относятся инертные газы — гелий, неон, аргон и так далее).

Итак, согласно модели идеального газа, его молекулы не взаимодействуют друг с другом. Поэтому внутренней энергией такого газа является сумма кинетических энергий хаотического движения всех его молекул или атомов. Следовательно, внутренняя энергия идеального одноатомного газа равна произведению средней кинетической энергии теплового движения молекул на их число:

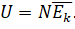
Число молекул в данной порции газа мы можем легко выразить из определения количества вещества:

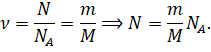
А значение средней кинетической энергии поступательного движения молекул мы распишем через постоянную Больцмана и абсолютную температуру:

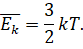
Перепишем формулу для внутренней энергии с учётом последних двух формул:

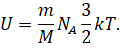
Теперь давайте с вами вспомним, что произведение постоянной Больцмана и числа Авогадро — это есть универсальная газовая постоянная R. Тогда получаем, что внутренняя энергия идеального одноатомного газа прямо пропорциональна его абсолютной температуре и не зависит от других макроскопических параметров системы:

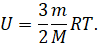
Для примера давайте с вами определим внутреннюю энергию неона массой 5 г, находящегося при температуре 27 ^оС.

Как правило, значение внутренней энергии в большинстве случаев вычислить очень трудно, поскольку каждое тело состоит из огромного числа частиц. Однако нас чаще будет интересовать не само значение внутренней энергии, а её изменение, которое происходит при переходе системы из одного состояния в другое.

Под приращением (или изменением) внутренней энергии понимают разность внутренних энергий системы в конечном и начальном состояниях:

∆U = U₂ – U₁.

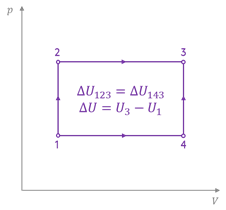
Например, переход некоторой массы идеального газа из состояния один в состояние три можно осуществить или в ходе изохорного нагревания и последующим изобарным расширением, или при изобарном расширении, а затем при изохорном нагревании. Однако изменение внутренней энергии газа и в одном и в другом случае будет одинаковым:

∆U₁₂₃ = ∆U₁₄₃ = U₃ – U₁.

Иными словами, внутренняя энергия является функцией состояния системы. Это означает, что изменение внутренней энергии при переходе термодинамической системы из одного состояния в другое зависит только лишь от значений параметров этих состояний, а не от процесса перехода.

В частности, изменение внутренней энергии данной масса идеального одноатомного газа происходит только при изменении его температуры:

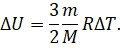
В качестве примера решим такую задачу. На рисунке в координатах (p, V) изображён процесс перехода идеального одноатомного газа определённой массы из состояния 1 в состояние 2. Определите приращение внутренней энергии газа, если его давление в конечном состоянии составляет 2 МПа, а объём в начальном состоянии был равен 3,0 л.

В заключении урока отметим, что при определении внутренней энергии реальных газов, жидкостей и твёрдых тел необходимо ещё учитывать и потенциальную энергию взаимодействия частиц, которая зависит от расстояния между ними. Поэтому в общем случае внутренняя энергия макроскопических тел зависит не только от абсолютной температуры, но и от объёма.

При изучении физики в восьмом классе вы узнали, что изменить состояние термодинамической системы можно двумя способами: используя теплопередачу или совершая работу. Процесс теплопередачи и совершение работы характеризуют соответственно физическими величинами — количеством теплоты Q и работой А, которые являются мерами изменения внутренней энергии системы.