Преобразование целого выражения в многочлен

Вопросы занятия:

·  ввести понятие «целое выражение»;

·  показать, что любое целое выражение можно представить в виде многочлена;

·  показать способ определения целого выражения;

·  показать способ преобразования целого выражения в многочлен стандартного вида.

Материал урока

В первую очередь необходимо выяснить, какие же выражения называют целыми.

Посмотрите внимательно на следующие выражения

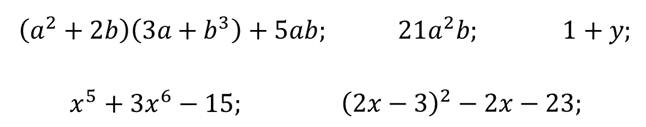
Они составлены из чисел и переменных с помощью действий сложения, вычитания и умножения. Также некоторые из выражений содержат степени.

Такие выражения называют целыми. Причём если выражение содержит, кроме действий сложения, вычитания и умножения, действие деление на число, не равное нулю, то оно также является целым, так как действие деление можно заменить умножением на число обратное делителю.

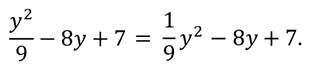
Следующее же выражение не является целым, так содержит деление на выражение с переменной.

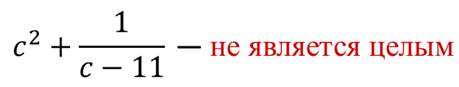
Обратите внимание, что среди целых выражений есть многочлены и одночлены.

Нам с вами известно, что сумму, разность и произведение многочленов можно преобразовать в многочлен. Поэтому любое целое выражение можно представить в виде многочлена.

Прежде, чем рассмотреть примеры преобразования целого выражения в многочлен, вспомним, что если перед скобками стоит знак плюс, то скобки можно опустить, сохранив знак каждого слагаемого, заключённого в скобки.

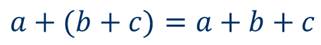
Если же перед скобками стоит знак минус, то скобки можно опустить, изменив знак каждого слагаемого, заключённого в скобки, на противоположный.

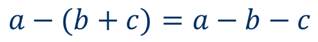
Также вспомним, что при умножении одночлена на многочлен надо умножить одночлен на каждый член многочлена.

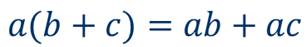
А при умножении многочлена на многочлен надо каждый член одного многочлена умножить на каждый член другого многочлена и полученные произведения сложить.

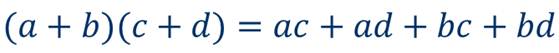
Ну а теперь давайте рассмотрим примеры.

Пример.

Пример.

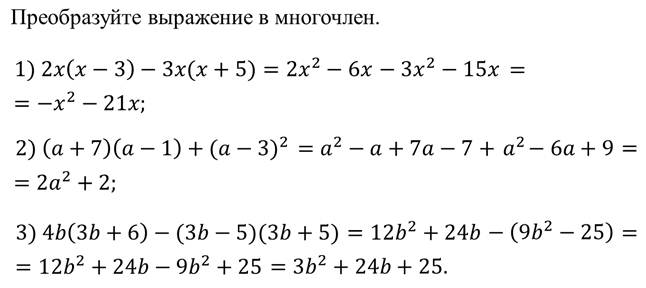
Пример.

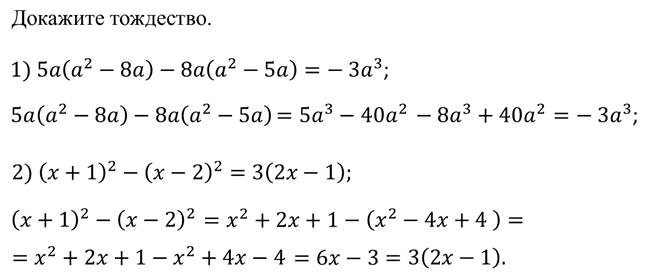
Итак, чтобы преобразовать целое выражение в многочлен, надо:

1.  раскрыть скобки, если они есть;

2.    применить формулы сокращённого умножения, если возможно;

3.    при необходимости привести подобные слагаемые, чтобы получить многочлен стандартного вида.

Помним, что многочленом стандартного вида называется многочлен, все члены которого имеют стандартный вид и среди них нет подобных.