Решение уравнений

Здравствуйте, ребята!

Сегодня я хочу вам напомнить о том, что такое уравнения, и как решать уравнения, в которых стоят знаки умножения и деления. А начну я с того, почему уравнение так называется.

Посмотрите на это слово – уравнение. В нем спрятан корень -равн-. И однокоренными к нему будут слова – равенство, равные, уравнять.

Уравнение – это математическое равенство, в котором есть одно или даже несколько неизвестных. Эти неизвестные обычно обозначаются буквами латинского алфавита (а + 12 = 17, 78 – в = 24, с – 32 = 19, х × 4 = 56, 98 : у = 7, k : 3 = 19, 3z – 2r = 2).

Видите, во всех этих записях стоит знак равно.

Это значит, что при решении уравнений надо найти такое значение неизвестного, при котором левая часть уравнения будет равна правой.

Вы уже умеете решать уравнения, в которых стоят знаки плюс или минус. Помните, для решения таких уравнений мы пользуемся правилами:

* Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое.

* Чтобы найти неизвестное уменьшаемое, надо сложить вычитаемое и разность.

* Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.

А ещё решать уравнения нам помогали схемы.

На первой из них видно, что слагаемые являются частями. Поэтому их мы находим вычитанием. Ведь если нам, например, надо взять часть яблока или груши, мы её отрежем, то есть вычтем.

А вот сумма – это целое, получить которое можно сложением частей.

Вторая схема нам подсказывает, что целым является уменьшаемое. А так как это целое, то его мы будем находить действием сложения. А вот вычитаемое – часть, поэтому его мы найдём вычитанием.

А как же решать уравнения, если в них не действия сложения или вычитания, а умножение и деление? Вот, например, такое уравнение.

х × 4 = 56

В нём надо найти такое значение икс, при умножении которого на четыре получится пятьдесят шесть. Ещё во втором классе мы с вами говорили о связи между компонентами и результатом действия умножения:

Если произведение двух множителей разделить на один из них, то получится другой множитель.

а ∙ b = с       с : b = а      с : a = b

Значит, неизвестный множитель надо находить действием деления. Найдём его. Решение будем записывать под уравнением.

Пишем: икс равен частному чисел пятьдесят шесть и четыре. Так-так, надо посчитать. Все расчёты можно записывать справа от уравнения.

Пятьдесят шесть это сорок и шестнадцать. Делим каждое на четыре. Десять и четыре. Четырнадцать. Отступаю клеточку вниз и пишу: икс равен четырнадцати. Но, конечно, не забываю и про проверку. Черта, под которой пишу наше уравнение точно такое же, как оно было записано в верхней строчке, только вместо буквы подставляю её значение. Получился решённый пример. Но мы обязательно должны проверить, правильно ли он решён. Для этого выполним действие, которое находится слева от знака равно. Умножим четырнадцать на шесть.

Полученное число пишем внизу под левой частью уравнения. А число из правой части уравнения просто переносим. Видите, результат действия в левой части и правая часть между собой равны. Значит, уравнение решено верно. Корень уравнения равен четырнадцати.

А как же решать уравнения, в которых стоит знак деления?

И тут нам на помощь придут правила связи между компонентами и результатом действия деления.

Вот посмотрите на это уравнение.

k : 3 = 19

В нём неизвестно делимое. Вспоминаем правило: Чтобы найти неизвестное делимое, надо частное умножить на делитель.

k : m = n      k = m ∙ n

Принимаемся за работу. К равно девятнадцать умножить на три. Получилось пятьдесят семь. Значит, k равно пятидесяти семи.

Подчёркиваю, и списываю наше уравнение, заменив букву k полученным значением. А теперь обязательно выполняю действие из левой части нашего уравнения. Пятьдесят семь разделить на три. Получилось девятнадцать. И справа тоже число девятнадцать. Есть равенство. Значит, уравнение решено верно и корень его равен пятидесяти семи.

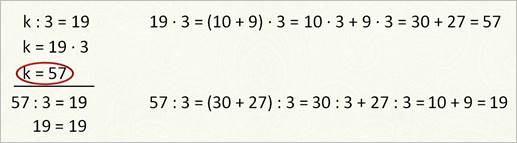
А если в уравнении на деление надо найти неизвестный делитель, как вот в этом уравнении?

98 : у = 7

И вновь на помощь приходит правило: Чтобы найти неизвестный делитель, надо делимое разделить на частное.

k : m = n      m = k : n

Решаем уравнение: 98 : у = 7.

Игрек равен частному чисел девяносто восемь и семь. Игрек равен четырнадцати. Проверяем. Записываем уравнение, заменив букву на число четырнадцать. Здесь придётся воспользоваться методом подбора, то есть умножить четырнадцать на такое однозначное число, чтобы в ответе получилось девяносто восемь. Но, так как справа записано число семь, попробую-ка я сразу умножить четырнадцать на семь. Отлично, произведение чисел четырнадцать и семь равно девяносто восьми. Все получилось. Корень уравнения равен четырнадцати.

Для решения этих уравнений мы воспользовались правилами связи между компонентами и результатом действий умножения и деления.

* Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.

* Чтобы найти неизвестный делитель, надо делимое разделить на частное.

* Чтобы найти неизвестное делимое, надо частное умножить на делитель.

Но вот некоторым ребятам бывает трудно запоминать все правила. А нельзя ли воспользоваться какой-нибудь короткой схемой, как мы это сделали при решении уравнений на сложение и вычитание? А почему бы и нет.

Для решения уравнений с действием умножения воспользуемся схемой, которой пользовались при решении уравнений, в которых стоит знак плюс. А для решения уравнений с действием деления воспользуемся схемой, которой пользовались при решении уравнений, в которых стоит знак минус. Просто заменим в схемах знаки.

Посмотрите, в первой схеме множители – это части, а произведение – целое. Части мы будем находить действием, обратным умножению – делением. А ведь наше правило об этом и говорит.

Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.

Вот, допустим, надо решить такое уравнение: три умножить на икс равно тридцать шесть.

3 ∙ х = 36

Подставляем его в нашу схему.

Икс – это часть. Находим делением. Икс равен двенадцати. Проверяем. Умножаем три на двенадцать. Тридцать шесть. И справа тридцать шесть. Уравнение решено верно. Схема работает!

А теперь проверим вторую схему. Игрек разделить на семь равно одиннадцать

Подставили его в схему.

Найти надо делимое. Это целое. Находим умножением. И правило об этом говорит.

Чтобы найти неизвестное делимое, надо частное умножить на делитель.

И здесь схема сработала. А справится ли наша схема с неизвестным делителем, попробуйте проверить сами. Решите вот это уравнение.

Ну вот и всё. Пришла пора нам с вами прощаться. Но я думаю, вы запомните правила, которые помогут вам решить любое уравнение.

* Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.

* Чтобы найти неизвестное делимое, надо частное умножить на делитель.

* Чтобы найти неизвестный делитель, надо делимое разделить на частное.

А если вдруг забудете его, вы всегда сможете воспользоваться схемами.

А я сегодня прощаюсь с вами. До встречи, ребята!