Призма. Площади поверхностей. Объём

Напомним, что призмой называется многогранник, у которого две грани – равные -угольники, лежащие в параллельных плоскостях (эти грани называются основаниями призмы), а остальные  граней – параллелограммы.

Эти параллелограммы называются боковыми гранями, а их стороны, не лежащие на основаниях призмы, называются боковыми рёбрами призмы.

Боковые рёбра призмы параллельны и равны.

Высотой призмы называется расстояние между основаниями.

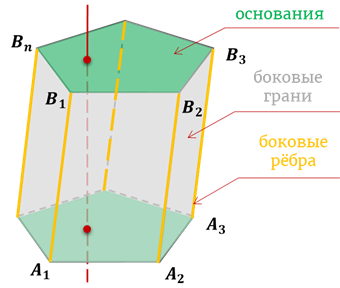
Площадью боковой поверхности призмы называется сумма площадей её боковых граней.

Площадью полной поверхности призмы – сумма площадей её боковых граней и двух площадей оснований.

Объём призмы равен произведению площади основания на высоту.

Призма, в зависимости от того, какой многоугольник лежит в основании, имеет своё название.

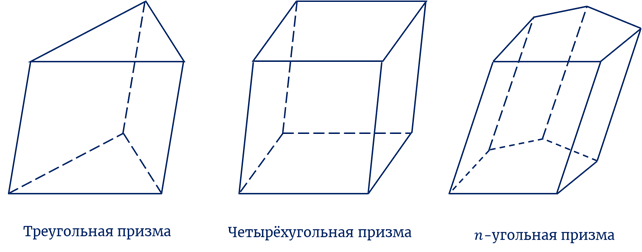
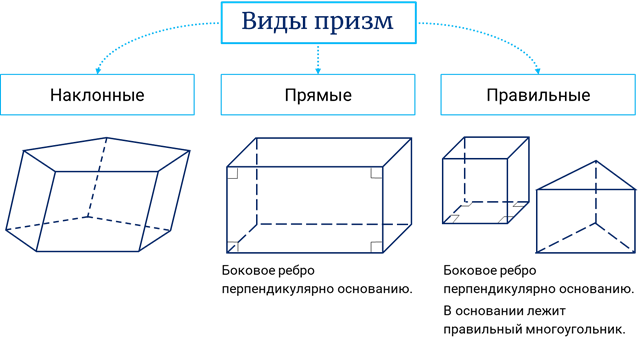
Рассмотрим наклонную призму. Здесь основания – равные многоугольники, лежащие в параллельных плоскостях. Боковые грани – параллелограммы. Высота призмы – перпендикуляр, опущенный из любой точки верхнего основания на плоскость нижнего. Боковые рёбра призмы равны и параллельны. Диагональ призмы соединяет две вершины, не лежащие в одной грани. Диагональное сечение проходит через два боковых ребра, не лежащих в одной грани, и является параллелограммом. Площадь боковой поверхности призмы равна сумме площадей боковых граней. Площадь полной поверхности равна сумме площади боковой поверхности и двух площадей оснований.

Рассмотрим прямую призму. Здесь боковые рёбра перпендикулярны основаниям. Боковые грани – прямоугольники. Высота равна боковому ребру. Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту (на боковое ребро).

И рассмотрим ещё правильную призму. Здесь в основании лежит правильный многоугольник. Боковые рёбра перпендикулярны основанию. Боковые грани – равные прямоугольники.

Основные моменты мы с вами повторили, а теперь давайте перейдём к практической части занятия.

Задача первая. В основании прямой четырёхугольной призмы лежит четырёхугольник со сторонами  см,  см,  см и  см. Высота призмы равна  см. Найдите площадь боковой поверхности призмы.

Решение.

Задача вторая. Дана шестиугольная наклонная призма с боковым ребром  см. Периметр сечения призмы плоскостью, перпендикулярной боковому ребру, равен  см. Найдите площадь боковой поверхности призмы.

Решение.

Задача третья. Дана прямая пятиугольная призма, в основание которой вписана окружность с радиусом  см. Площадь основания призмы равна  см², боковое ребро призмы равно  см. Найдите площадь боковой поверхности призмы.

Решение.

Задача четвёртая. Дана прямая четырёхугольная призма  В основании призмы лежит прямоугольная трапеция с основаниями  см,  см и , в которую можно вписать окружность. Диагональное сечение   призмы является квадратом. Найдите площадь полной поверхности призмы.

Решение.

Задача пятая. Диагональ правильной четырёхугольной призмы равна , диагональ боковой грани равна . Найдите площадь полной поверхности призмы.

Решение.

Задача шестая. Площадь боковой поверхности правильной четырёхугольной призмы равна  см². Диагональ боковой грани равна  см. Найдите наибольший возможный объём призмы, задаваемой этими условиями.

Решение.