Напомним, что призма, в основании которой лежит параллелограмм, называется параллелепипедом.
Стороны параллелограммов называются рёбрами параллелепипеда, а их вершины – вершинами параллелепипеда. Две грани параллелепипеда называются противолежащими, если они не имеют общего ребра.
Например,
грани 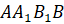 и
и
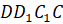 –
противолежащие.
–
противолежащие.
Грани,
имеющие общее ребро, называются смежными. Например, грани 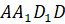 и
и
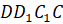 –
смежные, ребро
–
смежные, ребро 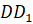 у
них общее.
у
них общее.
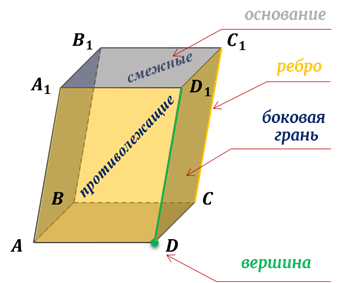
Иногда какие-нибудь две противолежащие грани параллелепипеда выделяются и называются основаниями, тогда остальные грани – боковыми гранями, а их стороны, соединяющие вершины оснований параллелепипеда, – его боковыми рёбрами.
В
нашем случае у параллелепипеда 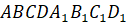 грани
грани
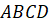 и
и
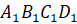 –
его основания. Остальные же грани являются боковыми гранями.
–
его основания. Остальные же грани являются боковыми гранями.
Две вершины параллелепипеда, не принадлежащие одной грани, называются противолежащими. Отрезок, соединяющий, противолежащие вершины, называется диагональю параллелепипеда. У параллелепипеда всего четыре диагонали.
Объединение боковых граней называется боковой поверхностью параллелепипеда, а объединение всех граней называется полной поверхностью параллелепипеда. Тогда площадью боковой поверхности параллелепипеда называется сумма площадей его боковых граней.
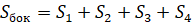
А площадью полной поверхности параллелепипеда называется сумма площадей всех его граней.
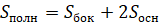
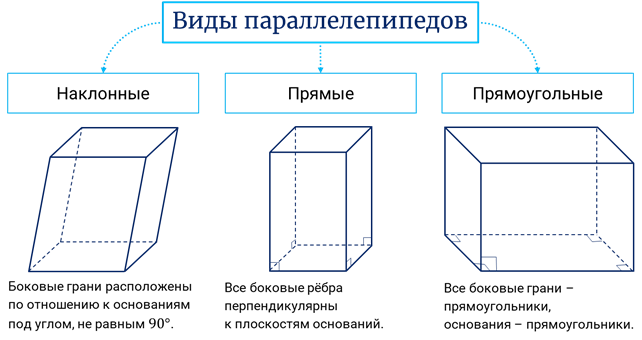
Параллелепипед обладает следующими свойствами:
1. Противолежащие грани параллелепипеда равны и лежат в параллельных плоскостях.
2. Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.
3. Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений.

Объём параллелепипеда равен произведению площади основания на высоту.
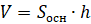
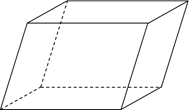
Объём прямоугольного параллелепипеда равен произведению трёх его измерений.
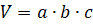
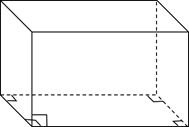
Куб – это прямоугольный параллелепипед, все рёбра которого равны, то есть все грани которого – равные квадраты.
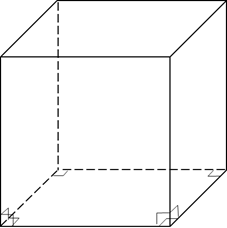
Диагональ
куба с ребром 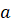 равна
равна
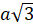 .
.
Объём
куба
равен 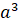 ,
где
,
где 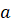 –
ребро куба.
–
ребро куба.
Основные моменты мы с вами повторили, а теперь давайте перейдём к практической части занятия.
Задача
первая. В основании прямого параллелепипеда лежит параллелограмм
с основаниями 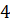 см
и
см
и 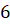 см
и острым углом
см
и острым углом 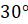 .
Боковое ребро параллелепипеда равно
.
Боковое ребро параллелепипеда равно 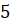 см.
Найдите площадь полной поверхности параллелепипеда.
см.
Найдите площадь полной поверхности параллелепипеда.
Решение.

Задача
вторая. Все грани параллелепипеда – ромбы с диагоналями 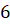 см
и
см
и 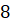 см.
Найдите площадь полной поверхности параллелепипеда.
см.
Найдите площадь полной поверхности параллелепипеда.
Решение.

Задача
третья. Найдите меньшую диагональ прямого параллелепипеда
высотой 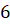 см
см
со сторонами основания 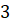 см
и
см
и 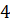 см
и углом между ними
см
и углом между ними 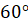 .
.
Решение.

Задача
четвёртая. В прямоугольном параллелепипеде 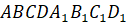 ребро
ребро
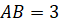 см,
см,
 см.
Найдите расстояние между диагональю параллелепипеда
см.
Найдите расстояние между диагональю параллелепипеда 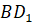 и
ребром
и
ребром 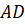 .
.
Решение.

Задача
пятая. Две стороны основания параллелепипеда равны 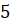 см
и
см
и 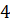 см,
угол между ними
см,
угол между ними 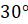 .
Боковое ребро равно
.
Боковое ребро равно 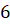 см
и наклонено к основанию под углом
см
и наклонено к основанию под углом 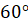 .
Найдите объём параллелепипеда.
.
Найдите объём параллелепипеда.
Решение.

Задача
шестая. Все грани параллелепипеда – ромбы с периметром
равным 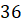 и
острым углом
и
острым углом 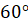 .
Найдите объём
.
Найдите объём 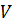 параллелепипеда.
В ответ запишите значение
параллелепипеда.
В ответ запишите значение 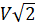 .
.
Решение.

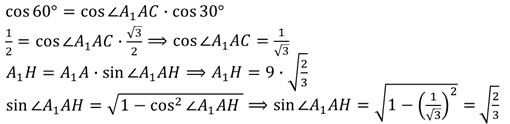
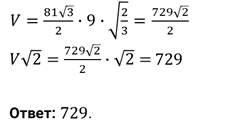

 Получите свидетельство
Получите свидетельство Вход
Вход




 11592
11592

