Задачи на встречное движение

Привет, ребята!

Ох и нагулялась я! Погода такая чудесная, снегу навалило! Я сегодня каталась на лыжах и увидела, как катались на коньках мальчик и девочка. Они бегали по ледяной дорожке навстречу друг другу. И тут я придумала про них задачи – задачи на встречное движение. А теперь хочу вас познакомить с этими задачами.

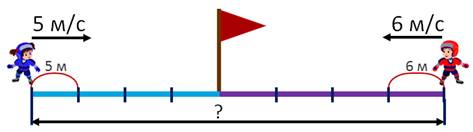
Вот посмотрите – это ледяная дорожка.

С противоположных её концов стояли девочка и мальчик. Они одновременно начали бежать навстречу друг другу. Девочка бежала со скоростью пять метров в секунду, а мальчик – со скоростью шесть метров в секунду, и через четыре секунды они встретились. Надо узнать длину ледяной дорожки.

Прежде всего надо выполнить чертёж.

Ледяную дорожку я уже нарисовала. Стрелочками отмечу направление движения конькобежцев. И над стрелками напишу скорость движения каждого конькобежца. Девочка бежала со скоростью пять метров в секунду, а мальчик – со скоростью шесть метров в секунду. Место их встречи обозначу флажком.

Ребята, вы помните? Когда мы выполняем чертёж в задачах на движение, расстояние делим на равные отрезки, каждый из которых обозначает отрезок пути, который пройден участником движения за одну единицу времени.

Так как в нашей задаче сказано, что ребята начали бежать одновременно и встретились через четыре секунды, значит, каждый из них бежал до встречи по четыре секунды. Расстояние, пройденное каждым до встречи, делим на четыре равных отрезка. А узнать надо длину всей дорожки.

Вот теперь можно приступать к решению.

Вся длина дорожки складывается из той части, которую пробежала девочка, и той, которую пробежал мальчик.

Сначала найдём расстояние, которое пробежала девочка до места встречи с мальчиком. Оно состоит из четырёх маленьких отрезочков, каждый из которых пройден за одну секунду. Скорость девочки – пять метров в секунду, значит, каждый такой отрезок равен пяти метрам. А весь участок пути до встречи находим действием умножения. По пять метров четыре раза. Двадцать метров пробежала девочка до встречи с мальчиком.

Теперь находим расстояние, которое пробежал мальчик до встречи. Его скорость – шесть метров в секунду. Значит, он бежал по шесть метров четыре раза. И пробежал до встречи двадцать четыре метра.

А теперь можно узнать и всю длину дорожки. Складываем отрезки пути, которые пробежали девочка и мальчик.

1) 5 · 4 = 20 (м) – пробежала девочка до встречи

2) 6 · 4 = 24 (м) – пробежал мальчик до встречи

3) 20 + 24 = 44 (м) – пробежали вместе

Ответ: длина ледяной дорожки – 44 м.

Длина ледяной дорожки – сорок четыре метра.

Эту задачу мы решили тремя действиями – сначала нашли расстояние, которое до встречи пробежала девочка, потом – то, что пробежал мальчик. А потом – длину всей дорожки. Но есть и другой способ решения такой задачи. Посмотрите на чертёж.

Если бы, например, девочка стояла, а мальчик бежал, то через секунду он бы приблизился к девочке на шесть метров. Ведь его скорость – шесть метров в секунду. Но ведь и девочка в это время не стояла на месте. Двигаться конькобежцы начали одновременно. Поэтому за первую секунду девочка пробежала пять метров, а мальчик – шесть метров. Вы видите, что за одну секунду они сблизились на одиннадцать метров. За следующую секунду они сблизятся ещё на одиннадцать метров. И так же за каждую секунду. Значит, одиннадцать метров в секунду – это скорость сближения конькобежцев.

А так как бежали они до встречи четыре секунды, то все расстояние, которое они вместе пробежали, найдём так: скорость сближения умножим на время.

1) 5 + 6 = 11 (м/с) – скорость сближения

2) 11 · 4 = 44 (м) – пробежали вместе

Ответ: длина ледяной дорожки – 44 м.

Ответ такой же, как и в первом способе решения, а действий – всего два.

Ну что же, вот вторая задача про наших конькобежцев.

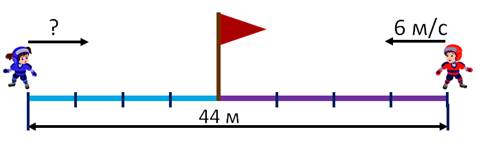
Длина ледяной дорожки – сорок четыре метра. С двух её противоположных концов одновременно навстречу друг другу побежали на коньках мальчик и девочка. Мальчик бежал со скоростью шесть метров в секунду, а девочка – со скоростью пять метров в секунду. Через сколько секунд они встретятся?

Выполняем чертёж к задаче.

Вот дорожка. Её длина – сорок четыре метра. Стрелочки, которые указывают направление движения конькобежцев, и над стрелочками – их скорость: пять метров в секунду и шесть метров в секунду. Флажок – место встречи. Найти надо время до встречи.

Давайте вспомним, как находится время в задачах на движение. Помните формулы?

Расстояние находится умножением, а скорость и время – делением. Чтобы найти время, надо расстояние разделить на скорость.

Но обратите внимание на то, что в задаче известно расстояние, которое конькобежцы пробежали совместно, а вот скорости – у каждого по отдельности.

Так делить недопустимо! Совместно пройденное расстояние можно делить только на совместную скорость. А вернее, такая скорость называется – скорость сближения. Скорость сближения – это сумма скоростей движущихся навстречу друг другу объектов.

Находим скорость сближения наших конькобежцев. Она равна одиннадцати метрам в секунду.

Вот теперь у нас есть совместно пройденное расстояние и скорость сближения. Можем находить время.

Делим расстояние на скорость.

1) 5 + 6 = 11 (м/с) – скорость сближения конькобежцев

2) 44 : 11 = 4 (с) – встретятся конькобежцы

Ответ: конькобежцы  встретятся через 4 с.

Всё верно. До встречи конькобежцы бежали четыре секунды.

Ну а теперь разберём ещё одну задачу про наших конькобежцев.

Длина ледяной дорожки – сорок четыре метра. С двух её противоположных концов одновременно навстречу друг другу побежали на коньках мальчик и девочка. Мальчик бежал со скоростью шесть метров в секунду. С какой скоростью бежала девочка, если конькобежцы встретились через четыре секунды?

И вновь выполняем чертёж.

Ледяная дорожка. Направление движения конькобежцев. Скорость мальчика. Скорость девочки нам пока неизвестна. Место встречи. Так как время до встречи – четыре секунды, расстояние, которое пробежал каждый конькобежец делим на четыре равные части.

Ну вот, чертёж готов. Приступаем к решению?

Эту задачу тоже можно решить двумя способами. Начнём так: у девочки мы знаем только время – четыре секунды. А вот у мальчика известны и скорость, и время. Зная их, можно найти расстояние, которое пробежал мальчик до встречи. Умножаем шесть на четыре. Двадцать четыре метра пробежал мальчик до места встречи.

Теперь можно узнать расстояние, которое пробежала девочка до встречи. Его мы можем найти вычитанием.

Теперь нам известно и расстояние до места встречи, которое пробежала девочка, и время. Можем найти скорость.

Делим расстояние на время.

1) 6 ∙ 4 = 24 (м) – пробежал мальчик до места встречи

2) 44 – 24 = 20 (м) – пробежала девочка до места встречи

3) 20 : 4 = 5 (м/с) – скорость девочки

Ответ: девочка бежала со скоростью 5 м/с.

Скорость девочки – пять метров в секунду.

Эту задачу можно решить и другим способом.

Зная расстояние, которое дети пробежали совместно и время до встречи, можно найти скорость сближения конькобежцев. Расстояние делим на время.

Я надеюсь, вы не забыли, что скорость сближения – это сумма скоростей движущихся навстречу друг другу объектов.

Из этой суммы вычитаем одно из слагаемых и получаем второе, то есть скорость девочки.

1) 44 : 4 = 11 (м/с) – скорость сближения конькобежцев

2) 11 – 6 = 5 (м/с) – скорость девочки

Ответ: девочка бежала со скоростью 5 м/с.

Этот способ решения короче, то есть он – рациональный. Но, конечно, каждый выбирает для себя тот способ решения, который для него удобнее и понятнее.

Сегодня мы с вами разобрали и решили три задачи на встречное движение. Я думаю,

вы уже поняли, что это были обратные задачи.

Не забудьте: решать задачи на движение вам помогут формулы.

И ещё сегодня я познакомила вас с понятием «скорость сближения» – это сумма скоростей движущихся навстречу друг другу объектов. Она нужна при решении задач, в которых известно совместно пройденное расстояние, но неизвестна одна из скоростей или, наоборот, известны скорости каждого участника движения по отдельности, а узнать нужно совместно пройденное расстояние.

Ну а если, решая какую-нибудь задачу на встречное движение, у вас появятся затруднения, вы можете пересмотреть ещё раз этот урок. Я уверена, после этого вы сможете разобраться в вашей трудной задаче. Только будьте внимательны!

А теперь пришла пора нам прощаться. Пока, ребята!