Перестановка и группировка множителей

А вы знаете, ребята, оказывается, в числовых выражениях, состоящих из нескольких множителей, числа могут прыгать, меняться местами, становиться парами. В общем, делают то, что им удобно.

И я сейчас расскажу вам о том, как можно выполнять перестановку и группировку множителей в числовых выражениях для того, чтобы удобно было находить их значения.

Но сначала давайте вспомним свойства умножения.

35 · 9 · 2 = 35 · 2 · 9

Вы догадались, какое это свойство? Конечно, переместительное! Для удобства вычисления множители переставили, поменяли местами.

А вот сейчас какое свойство применяется?

26 · 8 · 5 = 26 · (8 · 5)

Я думаю, что вы помните – это сочетательное свойство. Для удобства вычисления два соседних множителя заменили их произведением. То есть, как бы сгруппировали эти множители.

А сейчас я хочу показать вам вот такое числовое выражение:

25 · 14 · 5 · 4 =

Видите, в этом выражении только перестановки или только группировки множителей недостаточно для того, чтобы выполнить вычисление легко, без затруднений. Здесь нужно применить оба эти свойства умножения.

Так-так, надо подумать. Двадцать пять на четырнадцать умножать совсем неудобно. Если двадцать пять умножать на пять – тоже не очень удобное для дальнейшей работы число получится – сто двадцать пять.

А вот если двадцать пять умножить на четыре, получится сто. А любое число умножить на сто очень просто. И при умножении четырнадцати на пять тоже получится круглое число – семьдесят. Поэтому, переставив числа вот в таком порядке и сгруппировав их, мы получим числовое выражение, значение которого легко найти, выполнив вычисления в уме.

25 · 14 · 5 · 4 = (25 · 4) · (14 · 5) = 100 · 70 = 700

Правда, ведь так вычислять гораздо удобнее?

А теперь посмотрим вот на такое числовое выражение:

10 · 15 · 4 · 19 =

Я надеюсь, вы уже поняли: для того, чтобы умножение выполнить без особых затруднений, надо переставить и сгруппировать множители так, чтобы результаты в скобках были круглыми числами. Или хотя бы один из результатов.

Чтобы круглым получилось произведение с числом девятнадцать, вторым множителем может быть только число десять. И при умножении пятнадцати на четыре тоже получится круглое число. Это нам и надо.

10 · 15 · 4 · 19 = (10 · 19) · (15 · 4) = 190 · 60 = 11 400

Выполняем перестановку и группировку. Первое произведение равно ста девяноста, второе – шестидесяти. Перемножаем эти числа. Произведение равно одиннадцати тысячам четырёмстам.

А теперь попробуйте сами найти значение вот этих числовых выражений удобным способом.

9 · 6 · 5 · 3 =

2 · 10 · 35 · 8 =

45 · 8 · 2 · 4 =

27 · 8 · 4 · 3 =

Ну что, справились с заданием? Не всё получилось? Давайте проверять.

В первом выражении можно переставить и сгруппировать множители вот так:

9 · 6 · 5 · 3 = (9 · 3) · (6 · 5) = 27 · 30 = 810

При этом во второй скобке получается круглое число, и мы без особого труда умножим двадцать семь на тридцать.

Во втором выражении удобнее переставить и сгруппировать множители вот так:

2 · 10 · 35 · 8 = (2 · 35) · (10 · 8)

Или вот так:

2 · 10 · 35 · 8 = (10 · 8) · (2 · 35)

На результат в данных выражениях это не влияет. Выполняем вычисления.

2 · 10 · 35 · 8 = (10 · 8) · (2 · 35) = 80 · 70 = 5 600

И в первой, и во второй скобках получились круглые числа, которые легко перемножить.

Третье выражение:

45 · 8 · 2 · 4 = (45 · 2) · (8 · 4) = 90 · 32 = 2 880

А вот последнее, четвёртое выражение… Как ни старайся, при решении этого выражения ни перестановка, ни группировка множителей нам не поможет, так как в нём нет ни одной пары множителей, при умножении которых получится круглое число. Так что это выражение надо будет решать, записывая вычисления столбиком.

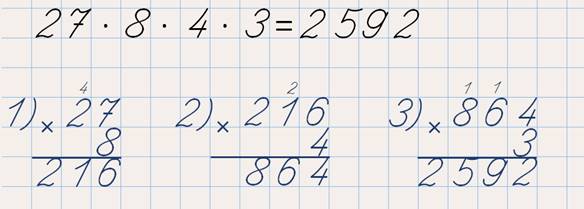
Ну вот и всё, о чём я сегодня с вами хотела поговорить.

Не забывайте, ребята:

Если числовое выражение состоит из нескольких множителей, можно выполнить перестановку и группировку этих множителей так, чтобы вычисление было удобно выполнять. Такой способ целесообразно применять в том случае, если при умножении хотя бы одной пары множителей получится круглое число.

Ну а теперь я прощаюсь с вами, ребята! Удачной работы!