Одно важное свойство окружности

«Ни тридцать лет, ни тридцать столетий не оказывают никакого влияния на ясность или красоту геометрических истин». Так сказал Чарльз Лютвидж Доджсон – английский математик, более известный во всем мире под псевдонимом Льюис Кэррол, автор известных произведений – «Алиса в Стране чудес» и «Алиса в Зазеркалье».

На предыдущих занятиях мы говорили о различных геометрических фигурах. И вы, конечно, уже поняли, что каждая из них обладает многими интересными свойствами. Некоторые из свойств оказываются присущими только этой фигуре, являются характерными только для неё. Используя эти свойства, можно совершенно иначе, с неожиданной точки зрения определить хорошо знакомую геометрическую фигуру.

Давайте с вами рассмотрим следующую задачу. Проведём на плоскости некоторую прямую. Возьмём на прямой какой-нибудь отрезок АB. Теперь проведём через точку А любую прямую и опустим из точки B перпендикуляр на эту прямую. Получим точку М. Из этой точки М мы видим отрезок АB под прямым углом.

Проведём другую прямую через точку А и опустим из точки B перпендикуляр на эту прямую. Получим точку 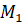. Из точки  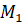мы видим отрезок АB под прямым углом.

Проведём ещё одну прямую через точку А и опустим на неё перпендикуляр из точки B. Получим точку 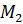. Из этой точки мы видим отрезок АB под прямым углом.

Если мы продолжим менять прямую, проходящую через точку А, то будем получать различные точки, которые будут описывать некоторую линию.

Оказывается, что эти точки будут описывать окружность, у которой отрезок АB является диаметром.

Давайте попробуем это объяснить. Достроим прямоугольный треугольник  до прямоугольника .

Отрезки  и  – диагонали прямоугольника .

Прямоугольник обладает тем свойством, что его диагонали равны между собой и делятся пополам в точке их пересечения.

Тогда, если точка О – середина отрезка АB (то есть середина диагонали), то отрезок ОМ равен половине диагонали прямоугольника, то есть . Значит, точка М лежит на окружности с центром в точке О и радиусом, равным .

Построим на отрезке АB как на диаметре окружность и возьмём на этой окружности произвольную точку М. На прямую АМ опустим перпендикуляр из точки B.

Как мы уже знаем, основание этого перпендикуляра должно лежать на окружности, а значит, оно должно совпасть с точкой М, так как прямая и окружность пересекаются не более чем в двух точках. Получается, что  – прямой. Отметим, что  называют углом, вписанным в окружность.

Таким образом, полученный результат можно сформулировать следующим образом. Вписанный в окружность угол, опирающийся на диаметр, равен .

На одном из занятий мы с вами с помощью циркуля и линейки проводили прямую, перпендикулярную данной прямой  через точку А, не лежащую на этой прямой.

Зная только что сформулированное свойство, мы можем выполнить следующее задание.

Дана прямая l и точка А, лежащая на ней. С помощью циркуля и линейки проведите через точку А прямую, перпендикулярную прямой l.

Отметим вне нашей прямой точку О. Затем построим окружность с центром в точке О, проходящую через точку А.

Вторую точку пересечения этой окружности с прямой обозначим буквой B. Через точку B проведём диаметр BC. Тогда прямая AC перпендикулярна прямой l, так как  – это угол, вписанный в окружность, опирающийся на диаметр.

Свойство угла, опирающегося на диаметр, является частным случаем следующего более общего свойства.

Возьмём окружность и две точки на ней – А и B. Оказывается, какую бы точку М на окружности по одну сторону от АB мы ни взяли, все образующиеся углы  будут равны между собой. Более того, если точка О (центр окружности) лежит с той же стороны от АB, что и точка М, угол  равен половине угла АOB.

Чтобы это объяснить, нам потребуются два факта.

Сумма углов треугольника равна .

Углы в равнобедренном треугольнике, лежащие против равных сторон, равны.

Итак, пусть точка О лежит внутри треугольника . Углы  и  обозначим соответственно через  и .

Рассмотрим треугольник АОМ. Он равнобедренный, так как стороны ОА и ОМ равны как радиусы окружности. Тогда углы ОМА и ОАМ равны как углы, лежащие против равных сторон. Каждый угол равен .

Так как сумма углов треугольника равна , то можем записать, что . Выразим из этого равенства угол AОМ: . Подставим  вместо углов ОМА и ОАМ: . Выполним преобразования и получим, что .

Рассмотрим треугольник . Он также является равнобедренным, так как стороны ОB и ОМ равны как радиусы окружности. Тогда углы ОМB и ОBМ равны как углы, лежащие против равных сторон. Каждый угол равен .

Сумма углов треугольника равна , тогда можем записать равенство: . Выразим из этого равенства угол BОМ: . Подставим  вместо углов ОМB и ОBМ:  . Выполним преобразования и получим, что .

Сумма трёх углов, сходящихся в точке О, равна . Тогда можем записать равенство: . Выразим из этого равенства угол : . Мы знаем, чему равны углы АОМ и BОМ. Подставим эти значения в равенство: . Выполним преобразования. И получим, что .

. Значит, угол АОB в 2 раза больше угла АМB. Или что то же самое: .

Таким образом, мы с вами объяснили сформулированное выше свойство.

Выполним задание. На окружности радиусом 3 см взяты три точки А, B и C так, чтобы угол АCB был равен . Найдите длину отрезка АB.

Решение.