Вы уже знаете, что симметрия в переводе с греческого означает «одинаковость в расположении частей». В таком широком понимании симметрия не имеет математического содержания.
Математики же вкладывают в понятие симметрии точный математический смысл, рассматривают специальные виды симметрии. Таким образом, симметрия становится мощным средством математических исследований, помогает решать сложные задачи.
Для того чтобы освоить «метод симметрии», надо сначала познакомиться с основными свойствами симметрии.
Итак, первое свойство. Для любой точки плоскости всегда можно построить симметричную ей точку относительно некоторой прямой.
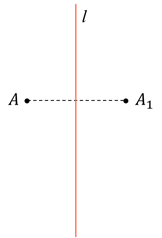
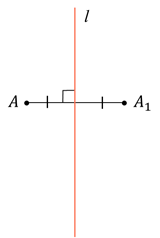
Второе свойство. На одном из предыдущих занятий мы строили с помощью угольника и линейки точку, симметричную данной точке относительно некоторой прямой, поэтому вы знаете, что отрезок, соединяющий симметричные точки, перпендикулярен оси симметрии и делится ею пополам.
Третье свойство. Если
отрезки 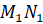 и
и 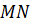 симметричны относительно прямой l, то их длины равны.
симметричны относительно прямой l, то их длины равны.
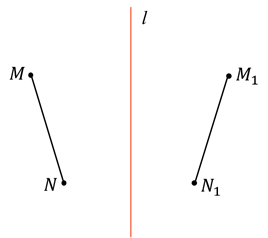
Четвёртое свойство. Если точка  симметрична точке
симметрична точке  относительно прямой l, то для любой точки
относительно прямой l, то для любой точки  на этой прямой отрезки
на этой прямой отрезки  и
и  равны.
равны.

Из этих свойств симметрии следует важное свойство плоскости.
Если  – некоторая точка плоскости, а
– некоторая точка плоскости, а  – точка на прямой l, то длина отрезка
– точка на прямой l, то длина отрезка  будет наименьшей, если отрезок
будет наименьшей, если отрезок  перпендикулярен прямой l.
перпендикулярен прямой l.
Другими словами, кратчайшим путём от точки до прямой является путь по перпендикулярному к этой прямой направлению.

Давайте докажем это.

Пусть дана прямая l и точка А, которая не лежит на этой прямой. Возьмём на прямой l точку B так, чтобы отрезок АB был перпендикулярен прямой l.
Пусть точка  – любая другая точка на прямой l. Нам надо доказать, что
отрезок
– любая другая точка на прямой l. Нам надо доказать, что
отрезок  меньше отрезка
меньше отрезка  .
.
Возьмём точку  , симметричную точке А относительно прямой l. Тогда точка B будет лежать на отрезке
, симметричную точке А относительно прямой l. Тогда точка B будет лежать на отрезке  . По второму свойству:
. По второму свойству:  . По четвёртому свойству:
. По четвёртому свойству:  .
.
Отрезок  короче ломаной
короче ломаной  . Следовательно, отрезок АB меньше отрезка
. Следовательно, отрезок АB меньше отрезка  . Что и требовалось доказать.
. Что и требовалось доказать.
Теперь начертим окружность с центром в точке А, проходящую через точку B. Получается, что АB – радиус этой окружности.

Эта окружность будет иметь с прямой l единственную общую точку – точку B. В этом случае говорят, что окружность касается прямой l или что прямая l является касательной к окружности.
Сформулируем важное свойство окружности и касательной к ней. Прямая, перпендикулярная радиусу окружности и проходящая через конец этого радиуса, касается окружности.
Сейчас мы с вами рассмотрим задачу, которая является классической задачей геометрии. Даны прямая l и две точки А и B по одну сторону от неё.

Найдите на прямой такую точку М, чтобы путь из точки А в точку B через точку М был кратчайшим, то есть длина ломаной АМB была наименьшей.
Данная задача решалась бы совсем легко, если бы точки А и B лежали по разные стороны от прямой l. Мы бы просто соединили эти точки отрезком и на пересечении с прямой l получили бы точку М.

Зная это, построим точку  симметричную точке А относительно прямой l. Затем соединим точку
симметричную точке А относительно прямой l. Затем соединим точку  и точку B.
и точку B.

Обозначим точку пересечения отрезка  с прямой l точкой М. Для точки
с прямой l точкой М. Для точки  , симметричной точке А относительно прямой l, длина отрезка
, симметричной точке А относительно прямой l, длина отрезка  равна длине отрезка
равна длине отрезка  . Значит,
. Значит,  . Тогда точка М и будет нужной нам точкой.
. Тогда точка М и будет нужной нам точкой.
Давайте выполним задание. Начертите прямоугольный
треугольник  , в котором угол
, в котором угол  прямой, а стороны
прямой, а стороны  и
и  равны соответственно 3 см и 2 см. Постройте треугольник,
симметричный данному относительно: а) прямой
равны соответственно 3 см и 2 см. Постройте треугольник,
симметричный данному относительно: а) прямой  ; б) прямой
; б) прямой  ; в) прямой
; в) прямой  . Какой фигурой в каждом случае является объединение данного
треугольника и построенного?
. Какой фигурой в каждом случае является объединение данного
треугольника и построенного?
Решение.







 Получите свидетельство
Получите свидетельство Вход
Вход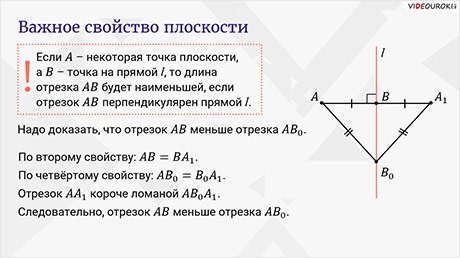




 2864
2864

